练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知对数函数y=logax在区间[3，6]上的最大值比最小值大2，则实数a=$\sqrt{2}$或$\frac{\sqrt{2}}{2}$．

    分析 利用函数的单调性求出函数的最大值和最小值列出不等式解出．需要分情况讨论．

    解答 解：（1）当a＞1时，y=logax在区间[3，6]上是增函数，
    ymax=loga6，ymin=loga3
    ∴loga6-loga3=2，
    即loga2=2，解得a=$\sqrt{2}$．
    （2）当0＜a＜1时，y=logax在区间[3，6]上是减函数，
    ymax=loga3，ymin=loga6
    ∴loga3-loga6=2，
    即loga$\frac{1}{2}$=2，解得a=$\frac{\sqrt{2}}{2}$．
    故答案为$\sqrt{2}$或$\frac{\sqrt{2}}{2}$．

    点评 本题考查了对数函数的单调性的应用，注意分情况讨论，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．函数f（x）=2x2-2x的单调递增区间是（　　）
    A．（-∞，1]B．[1，+∞）C．（-∞，2]D．[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

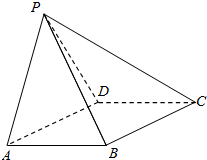    9．如图所示，在四棱锥P-ABCD中，四边形ABCD为菱形，∠DAB=60°，AB=2，△PAD为等边三角形，平面PAD⊥平面ABCD．
    （1）求证AD⊥PB．
    （2）在棱AB上是否存在点F，使DF与平面PDC所成角的正弦值为$\frac{2\sqrt{5}}{5}$？若存在，确定线段AF的长度；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图是一梯形OABC的直观图．其直观图面积为S，求梯形OABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设f（x）=logag（x）（a＞0，且a≠1）
    （1）若f（x）=log${\;}_{\frac{1}{2}}$（3x-1），且满足f（x）＞1，求x的取值范围：
    （2）若g（x）=ax2-x，是否存在实数a使得f（x）在区间[$\frac{1}{2}$，3]上是增函数？如果存在，说明a可以取哪些值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．求函数y=acosx+b（a＜0）的最大值与最小值及相应的x值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．点A（2，-1）与B（4，3）的中点坐标是（3，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．为了整顿道路交通秩序，某地考虑对行人闯红灯进行处罚，为更加详细闯红灯人数的作用，在某一个路口进行了五天试验，得到当天的处罚金额与当天闯红灯人数
    当天处罚金额x（单位：元）05101520
    当天闯红灯的人数y8050402010
    （1）根据以上数据，建立当天闯红灯人数y关于当天处罚金额x的回归直线方程；
    （2）根据统计数据，上述路口每天经过的行人约为400人，每人闯红灯的可能性相同，在行0元处罚的情况下，记甲、乙、丙三人中闯红灯的人数为X，求X的分布列和数学期望相互独立）．
    附：回归直线方程中系数计算公式b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}$，$\overline{a}$=$\overline{y}$-b$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．曲线y=$\frac{1}{2}$x2+x在点（2，4）处的切线与坐标轴围成的三角形面积为$\frac{2}{3}$．

    查看答案和解析>>

    同步练习册答案