
【题目】如图所示,在正方体ABCD-A′B′C′D′中:
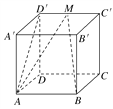
(1)求二面角D′-AB-D的大小;
(2)若M是C′D′的中点,求二面角M-AB-D的大小.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据二面角定义,可得∠D′AD为二面角D′-AB-D的平面角,再根据正方体的性质即可求解;
(2)取AB的中点N,连接MN,则MN⊥AB.取CD的中点H,连接HN,则HN⊥AB,从而∠MNH是二面角M-AB-D的平面角,再根据正方体的性质即可求解.
试题解析:
(1)在正方体ABCD-A′B′C′D′中,AB⊥平面ADD′A′,所以AB⊥AD′,AB⊥AD,因此∠D′AD为二面角D′-AB-D的平面角,在Rt△D′DA中,∠D′AD=45°,所以二面角D′-AB-D的大小为45°.
(2)因为M是C′D′的中点,所以MA=MB,取AB的中点N,连接MN,则MN⊥AB.取CD的中点H,连接HN,则HN⊥AB.
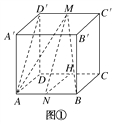
从而∠MNH是二面角M-AB-D的平面角.∠MNH=45°,所以二面角M-AB-D的大小为45°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 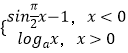 (a>0且a≠1)的图象上关于y轴对称的点至少有3对,则实数a的范围是( )
(a>0且a≠1)的图象上关于y轴对称的点至少有3对,则实数a的范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为F(1,0),点P是椭圆C上一动点,若动点P到点的距离的最大值为b2 .
的右焦点为F(1,0),点P是椭圆C上一动点,若动点P到点的距离的最大值为b2 .
(1)求椭圆C的方程,并写出其参数方程;
(2)求动点P到直线l:x+2y﹣9=0的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥P﹣ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( ) 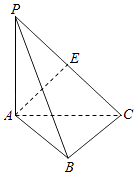
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.

(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=sinx+ ![]() cosx的图象向右平移φ(φ>0)个单位长度得到函数y=sinx﹣
cosx的图象向右平移φ(φ>0)个单位长度得到函数y=sinx﹣ ![]() cosx的图象,则φ的最小值为( )
cosx的图象,则φ的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
问:(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
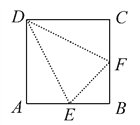
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:函数f(x)=log2m(x+1)是增函数;命题Q:x∈R,x2+mx+1≥0.
(1)写出命题Q的否命题¬Q;并求出实数m的取值范围,使得命题¬Q为真命题;
(2)如果“P∨Q”为真命题,“P∧Q”为假命题,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线a,b和平面M,N,且a⊥M,则下列说法正确的是 ( )
A. b∥Mb⊥a B. b⊥ab∥M
C. N⊥Ma∥N D. aNM∩N≠
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com