
分析 (1)由题意可得2x-1≥3,或 2x-1≤-3,从而求得x的范围.
(2)构造函数y=|x-3|+|x+1|=$\left\{\begin{array}{l}{-2x+2,x≤-1}\\{4,-1<x<3}\\{2x-2,x≥3}\end{array}\right.$,令y=6,求得x的值,可得不等式的解集.
解答 (1)解:∵|2x-1|≥3,∴2x-1≥,或 2x-1≤-3,
求得x≤-1或 x≥2,故不等式的解集为{x|x≤-1或 x≥2 }.
(2)解:构造函数y=|x-3|+|x+1|=$\left\{\begin{array}{l}{-2x+2,x≤-1}\\{4,-1<x<3}\\{2x-2,x≥3}\end{array}\right.$,
令y=6,求得x=4或x=-2,
故|x-3|+|x+1|<6的解集为(-2,4).
点评 本题主要考查分式不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.


 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $|\overrightarrow a|=\sqrt{{{(\overrightarrow a)}^2}}$ | B. | λ($\overrightarrow a$•$\overrightarrow b$)=$\overrightarrow a$•(λ$\overrightarrow b$) | C. | ($\overrightarrow a$-$\overrightarrow b$)$\overrightarrow c$=$\overrightarrow a$•$\overrightarrow c$-$\overrightarrow b$•$\overrightarrow c$ | D. | $\overrightarrow a$与$\overrightarrow b$共线?$\overrightarrow a$•$\overrightarrow b$=$|{\overrightarrow a}||{\overrightarrow b}|$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 由于当前学生课业负担重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图:请指出这组数据的中位数为4.75.
由于当前学生课业负担重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图:请指出这组数据的中位数为4.75.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
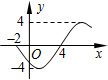 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<π)的部分图象如图所示,则该函数的解析式为f(x)=4sin($\frac{π}{6}$x-$\frac{2π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{4}{3},\frac{3}{2}}]$ | B. | $[{\frac{1}{3},2}]$ | C. | $[{\frac{4}{3},3}]$ | D. | $[{\frac{3}{2},3}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com