
 如图,椭圆
如图,椭圆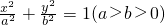 的左焦点为F,过点F的直线交椭圆于A,B两点.当直线AB经过椭圆的一个顶点时,其倾斜角恰为60°.
的左焦点为F,过点F的直线交椭圆于A,B两点.当直线AB经过椭圆的一个顶点时,其倾斜角恰为60°. 的取值范围.
的取值范围.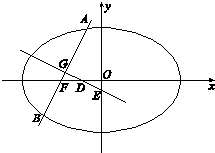 解:(Ⅰ)依题意,当直线AB经过椭圆的顶点(0,b)时,其倾斜角为60°.
解:(Ⅰ)依题意,当直线AB经过椭圆的顶点(0,b)时,其倾斜角为60°. .
.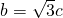 代入a2=b2+c2,得a=2c.
代入a2=b2+c2,得a=2c.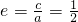 .
.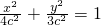 ,设A(x1,y1),B(x2,y2).
,设A(x1,y1),B(x2,y2).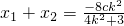 ,
, ,所以
,所以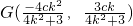 .
.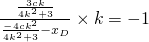 ,
,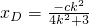 .
.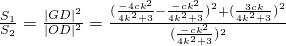 =
=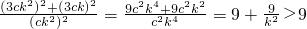 .
. 的取值范围是(9,+∞).
的取值范围是(9,+∞).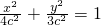 ,设A(x1,y1),B(x2,y2).由题意直线AB不能与x,y轴垂直,故设直线AB的方程为y=k(x+c),将其代入椭圆方程消掉y变为关于x的二次方程,由韦达定理及中点坐标公式可用k,c表示出中点G的坐标,由GD⊥AB得kGD•k=-1,则D点横坐标也可表示出来,易知△GFD∽△OED,故
,设A(x1,y1),B(x2,y2).由题意直线AB不能与x,y轴垂直,故设直线AB的方程为y=k(x+c),将其代入椭圆方程消掉y变为关于x的二次方程,由韦达定理及中点坐标公式可用k,c表示出中点G的坐标,由GD⊥AB得kGD•k=-1,则D点横坐标也可表示出来,易知△GFD∽△OED,故 =
=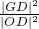 ,用两点间距离公式即可表示出来,根据式子结构特点可求得
,用两点间距离公式即可表示出来,根据式子结构特点可求得 的范围;
的范围;

 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
(本小题满分16分)
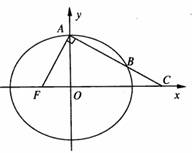 如图,椭圆
如图,椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线分别交椭圆、
的垂线分别交椭圆、![]() 轴于
轴于![]() 两点.⑴若
两点.⑴若![]() ,求实数
,求实数![]() 的值;
的值;
⑵设点![]() 为
为![]() 的外接圆上的任意一点,
的外接圆上的任意一点,
当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省“十二校”高三第2次联考文科数学试卷(解析版) 题型:解答题
如图,椭圆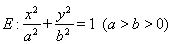 的左焦点为
的左焦点为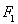 ,右焦点为
,右焦点为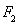 ,过
,过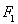 的直线交椭圆于
的直线交椭圆于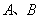 两点,
两点,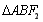 的周长为8,且
的周长为8,且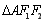 面积最大时,
面积最大时,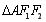 为正三角形.
为正三角形.

(1)求椭圆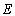 的方程;
的方程;
(2)设动直线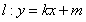 与椭圆
与椭圆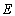 有且只有一个公共点
有且只有一个公共点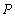 ,且与直线
,且与直线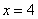 相交于点
相交于点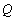 ,证明:点
,证明:点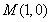 在以
在以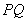 为直径的圆上.
为直径的圆上.
查看答案和解析>>
科目:高中数学 来源:2014届四川成都六校协作体高二下学期期中考试理科数学试卷(解析版) 题型:解答题
如图,椭圆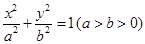 的左焦点为
的左焦点为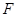 ,过点
,过点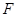 的直线交椭圆于
的直线交椭圆于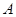 ,
,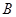 两点.当直线
两点.当直线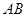 经过椭圆的一个顶点时,其倾斜角恰为
经过椭圆的一个顶点时,其倾斜角恰为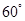 .
.
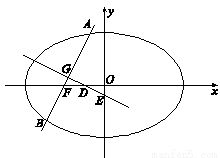
(Ⅰ)求该椭圆的离心率;
(Ⅱ)设线段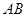 的中点为
的中点为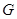 ,
,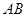 的中垂线与
的中垂线与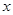 轴和
轴和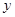 轴分别交于
轴分别交于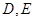 两点,
两点,
记△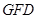 的面积为
的面积为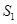 ,△
,△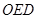 (
(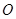 为原点)的面积为
为原点)的面积为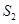 ,求
,求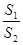 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省苏州市高三(上)期末数学试卷(解析版) 题型:解答题
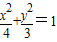 的左焦点为F,上顶点为A,过点A作直线AF的垂线分别交椭圆、x轴于B,C两点.
的左焦点为F,上顶点为A,过点A作直线AF的垂线分别交椭圆、x轴于B,C两点.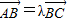 ,求实数λ的值;
,求实数λ的值;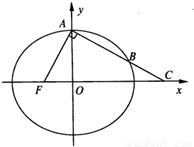
查看答案和解析>>
科目:高中数学 来源:2013年上海市崇明县高考数学一模试卷(文科)(解析版) 题型:解答题
 的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com