
分析 (1)运用数量积得出$\overrightarrow{a}$$•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos$<\overrightarrow{a}$,$\overrightarrow{b}$>,利用三角函数有界性求解证明||cos$<\overrightarrow{a}$,$\overrightarrow{b}$>|<1,即可得证|$\overrightarrow{a}•\overrightarrow{b}$|<|$\overrightarrow{a}$||$\overrightarrow{b}$|;
(2)化简得出2y-1=ycosx+sinx,转化为数量积$\overrightarrow{a}$=(cosx,sinx),$\overrightarrow{b}$=(y,1),根据:$\overrightarrow{a}•\overrightarrow{b}$=ycisx+sinx,|$\overrightarrow{a}$=1,|$\overrightarrow{b}$|=$\sqrt{{y}^{2}+1}$,利用|$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$|可以多次需要的不等式.
解答 解:(1)∵$\overrightarrow{a}$$•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos$<\overrightarrow{a}$,$\overrightarrow{b}$>,
∴|$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$||cos$<\overrightarrow{a}$,$\overrightarrow{b}$>|,
∵向量$\overrightarrow{a}$,$\overrightarrow{b}$是两个不共线的向量.
∴||cos$<\overrightarrow{a}$,$\overrightarrow{b}$>|<1,
∴|$\overrightarrow{a}•\overrightarrow{b}$|<|$\overrightarrow{a}$||$\overrightarrow{b}$|;
(2)∵y=$\frac{1+sinx}{2-cosx}$,
∴2y-1=ycosx+sinx,
令$\overrightarrow{a}$=(cosx,sinx),$\overrightarrow{b}$=(y,1),
根据:$\overrightarrow{a}•\overrightarrow{b}$=ycisx+sinx,|$\overrightarrow{a}$=1,|$\overrightarrow{b}$|=$\sqrt{{y}^{2}+1}$,
|$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$|,即|2y-1|≤1×$\sqrt{{y}^{2}+1}$,
化简得出:3y2-4y≤0,即0≤y$≤\frac{4}{3}$,
∴最大值为:$\frac{4}{3}$
点评 本题考察了平面向量的数量积的运用,不等式的运用,函数的性质值域等知识的综合,属于中档题.


科目:高中数学 来源: 题型:选择题
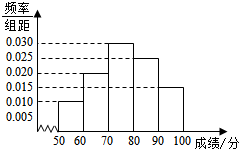 对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )
对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )| A. | 0.09 | B. | 0.20 | C. | 0.25 | D. | 0.40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
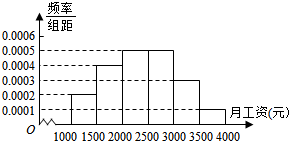 进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).
进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π-α | B. | α | C. | $\frac{π}{2}$-α | D. | $\frac{3π}{2}$-α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 等腰梯形 | D. | 不等腰梯形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com