
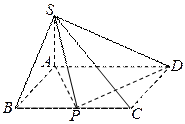
 如图,四棱锥
如图,四棱锥 的底面是矩形,
的底面是矩形, 底面
底面 ,P为BC边的中点,SB与
,P为BC边的中点,SB与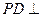 平面SAP;
平面SAP;
 底面
底面 ,
,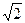 ,……………………….2分
,……………………….2分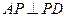 .………….…….3分
.………….…….3分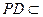 平面ABCD,
平面ABCD,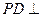 平面SAP.…………………………….5分
平面SAP.…………………………….5分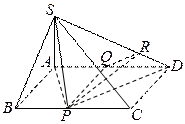 (2)设Q为AD的中点,连结PQ, ………………….………6分
(2)设Q为AD的中点,连结PQ, ………………….………6分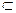 平面SAD,则平面SAD⊥平面PAD….7分
平面SAD,则平面SAD⊥平面PAD….7分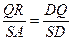
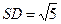 ,所以
,所以 ….……….10分
….……….10分 ………11分
………11分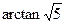 .……………….…….…….12分
.……………….…….…….12分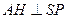 ,且垂足为H,在平面SAD内作
,且垂足为H,在平面SAD内作 ,且垂足为E,连接HE,
,且垂足为E,连接HE,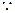
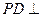 平面SAP。
平面SAP。
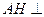 平面SPD…………7分
平面SPD…………7分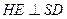
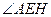 是二面角A-SD-P的平面角……………………………….9分
是二面角A-SD-P的平面角……………………………….9分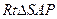 中,
中, ,在
,在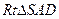 中,
中,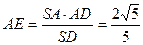 ,
,
 . ………………………………….11分
. ………………………………….11分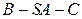 的大小为
的大小为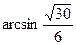 ……………………………12分
……………………………12分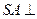 底面
底面 ,
, 由已知∠SBA=45°,所以AB=SA=1
由已知∠SBA=45°,所以AB=SA=1 ,
,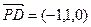 ,
, ..………….…....3分
..………….…....3分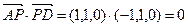 ,
, =0。
=0。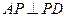 ,
,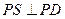
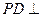 平面SAP ………….……………..….…5分
平面SAP ………….……………..….…5分
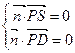 ,得
,得 解得
解得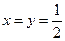 ,
, ……………….…………….……….8分
……………….…………….……….8分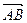 是平面SAD的法向量,易得
是平面SAD的法向量,易得 …9分
…9分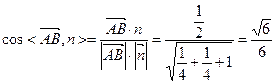 ….………………….11分
….………………….11分 的大小为
的大小为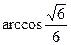 . ……………….……….…… 12分
. ……………….……….…… 12分

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
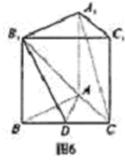
 中,侧面
中,侧面
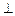 底面
底面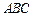 ,
,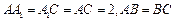 ,
, ,O为
,O为 中点.
中点.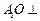 平面
平面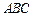 ;
;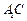 与平面
与平面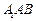 所成角的正弦值;
所成角的正弦值;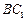 上是否存在一点
上是否存在一点 ,使得
,使得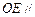 平面
平面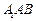 ,若不存在,说明理由;若存在,
,若不存在,说明理由;若存在, 的位置.
的位置.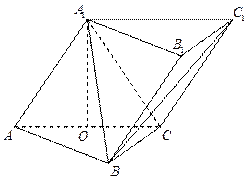
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
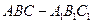 中,
中,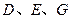 分别是
分别是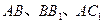 的中点,
的中点,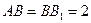 .
.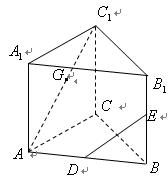
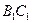 上是否存在点
上是否存在点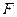 使
使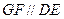 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;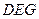 与底面
与底面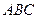 所成锐二面角的正切值;
所成锐二面角的正切值;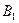 到截面
到截面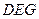 的距离.
的距离.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
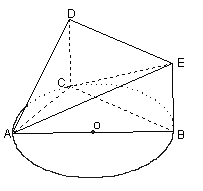
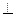 平面ABC ,
平面ABC ,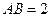 ,
,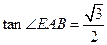 .
.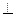 平面
平面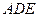 ;
;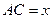 ,
,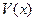 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求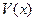 的表达式;
的表达式;
 (3)当
(3)当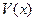 取得最大值时,求证:AD=CE.
取得最大值时,求证:AD=CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com