【题目】已知数列
为等差数列，
，
.
（1） 求数列的通项公式;
（2）求数列
的前n项和
.
【答案】（1）
；（2）
.
【解析】试题分析：利用等差数列通项公式列出方程组，求出首项和公差，由此能求出数列
的
通项公式；（2）由（1）可得
，利用错位相减法及等比数列前
项和公式能求出数列
的前n项和
.
试题解析： (1)设数列
的公差为
，依题意得方程组
解得
.
所以的通项公式为
.
（2）由（1）可得，
－得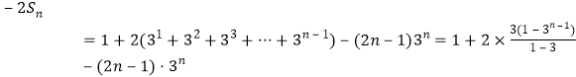
所以
.
【 方法点睛】本题主要考查等差数列的通项公式、等比数列的求和公式以及错位相减法求数列的前 项和，属于中档题.一般地，如果数列是等差数列，
是等比数列，求数列
的前项和时，可采用“错位相减法”求和，一般是和式两边同乘以等比数列的公比，然后作差求解, 在写出“”
与“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
”的表达式.
期末宝典单元检测分类复习卷系列答案科目：高中数学 来源： 题型：
【题目】已知椭圆
＋
＝1(a>b>0)的焦点分别为F1(0，－1)，F2(0,1)，且3a2＝4b2.
(1)求椭圆的方程；
(2)设点P在这个椭圆上，且|PF1|－|PF2|＝1，求∠F1PF2的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．
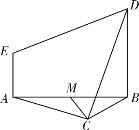
(1)证明：CM⊥DE；
(2)在边AC上找一点N，使CD∥平面BEN.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明，得到如下列联表：
男 | 女 | 总计 | ||
读营养说明 | 16 | 28 | 44 | |
不读营养说明 | 20 | 8 | 28 | |
总计 | 36 | 36 | 72 |
(1)根据以上列联表判断，能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢？
(2)从被询问的28名不读营养说明的大学生中，随机抽取2名学生，求抽到女生人数
的分布列及数学期望.
附：
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于定义域为
的函数
，如果同时满足以下三条：①对任意的
，总有
；②
；③若
，都有
成立，则称函数为理想函数．
(1) 若函数为理想函数，求
的值；
(2)判断函数
是否为理想函数，并予以证明；
(3) 若函数为理想函数，
假定
，使得
，且
，求证：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
，其中
，若
、
、
是
的三条边长，则下列结论：①对于一切
都有
；②存在
使
、
、
不能构成一个三角形的三边长；③为钝角三角形，存在
，使
，其中正确的个数为______个
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某厂生产某种产品的年固定成本为250万元，每生产
千件，需另投入成本
，当年产量不足80千件时，
（万元）；当年产量不小于80千件时，
（万元），每件售价为0.05万元，通过市场分析，该厂生产的商品能全部售完．
（1）写出年利润
（万元）关于年产量（千件）的函数解析式；
（2）年产量为多少千件时，该厂在这一商品的生产中所获利润最大？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=
（c为常数），且f（1）=0．
（1）求c的值；
（2）证明函数f（x）在[0，2]上是单调递增函数；
（3）已知函数g（x）=f（ex），判断函数g（x）的奇偶性．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
