
【题目】已知![]() ,函数
,函数![]() (其中
(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若当![]() 时都有
时都有![]() 成立,求整数
成立,求整数![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-ax-1(e为自然对数的底数),a>0.
(1)若函数f(x)恰有一个零点,证明:aa=ea-1;
(2)若f(x)≥0对任意x∈R恒成立,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“二万五千里长征”是1934年10月到1936年10月中国工农红军进行的一次战略转移,是人类历史上的伟大奇迹,向世界展示了中国工农红军的坚强意志,在期间发生了许多可歌可泣的英雄故事.在中国共产党建党![]() 周年之际,某中学组织了“长征英雄事迹我来讲”活动,已知该中学共有高中生
周年之际,某中学组织了“长征英雄事迹我来讲”活动,已知该中学共有高中生![]() 名,用分层抽样的方法从该校高中学生中抽取一个容量为
名,用分层抽样的方法从该校高中学生中抽取一个容量为![]() 的样本参加活动,其中高三年级抽了
的样本参加活动,其中高三年级抽了![]() 人,高二年级抽了
人,高二年级抽了![]() 人,则该校高一年级学生人数为( )
人,则该校高一年级学生人数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若曲线![]() 上一点
上一点![]() 的极坐标为
的极坐标为![]() ,且
,且![]() 过点
过点![]() ,求
,求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,椭圆
轴的正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程(写成一般式)和椭圆
的普通方程(写成一般式)和椭圆![]() 的直角坐标方程(写成标准方程);
的直角坐标方程(写成标准方程);
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个排球队在采用![]() 局
局![]() 胜制排球决赛中相遇,已知每局比赛中甲获胜的概率是
胜制排球决赛中相遇,已知每局比赛中甲获胜的概率是![]() .
.
(1)求比赛进行了![]() 局就结束的概率;
局就结束的概率;
(2)若第![]() 局甲胜,两队又继续进行了
局甲胜,两队又继续进行了![]() 局结束比赛,求
局结束比赛,求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)直线l的参数方程为![]() ,(t为参数),直线l与x轴交于点F,与曲线C的交点为A,B,当
,(t为参数),直线l与x轴交于点F,与曲线C的交点为A,B,当![]() 取最小值时,求直线l的直角坐标方程.
取最小值时,求直线l的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验,某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月的市场占有率![]() 进行了统计,结果如表:
进行了统计,结果如表:
月份 |
|
|
|
|
|
|
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 11 | 13 | 16 | 15 | 20 | 21 |
![]() 请用相关系数说明能否用线性回归模型拟合y与月份代码x之间的关系,如果能,请计算出y关于x的线性回归方程,并预测该公司2018年12月的市场占有率
请用相关系数说明能否用线性回归模型拟合y与月份代码x之间的关系,如果能,请计算出y关于x的线性回归方程,并预测该公司2018年12月的市场占有率![]() 如果不能,请说明理由.
如果不能,请说明理由.
![]() 根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元
根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元![]() 辆和800元
辆和800元![]() 辆的A,B两款车型,报废年限各不相同
辆的A,B两款车型,报废年限各不相同![]() 考虑公司的经济效益,该公司决定对两款单车进行科学模拟测试,得到两款单车使用寿命频数表如表:
考虑公司的经济效益,该公司决定对两款单车进行科学模拟测试,得到两款单车使用寿命频数表如表:
报废年限 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 10 | 30 | 40 | 20 | 100 |
B | 15 | 40 | 35 | 10 | 100 |
经测算,平均每辆单车每年可以为公司带来收入500元![]() 不考虑除采购成本以外的其他成本,假设每辆单车的使用寿命都是整数年,用频率估计每辆车使用寿命的概率,分别以这100辆单车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择釆购哪款车型?
不考虑除采购成本以外的其他成本,假设每辆单车的使用寿命都是整数年,用频率估计每辆车使用寿命的概率,分别以这100辆单车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择釆购哪款车型?
参考数据:![]() ,
,![]() ,
,![]()
参考公式:相关系数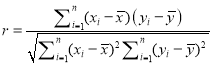
回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为: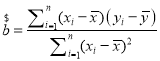 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com