【题目】已知a＝(1，2)，b＝(－2，n)，a与b的夹角是45°.
(1) 求b；
(2) 若c与b同向，且a与c－a垂直，求向量c的坐标．
【答案】（1）(－2，6)．（2）(－1，3)
【解析】试题分析（1）由向量夹角公式、向量模的坐标表示、向量数量积的坐标表示得关于n的方程，解方程可得n＝6，即得b；（2）由向量平行可设c＝λb(λ>0)，由向量垂直可得数量积为零，根据向量数量积坐标表示可得关于λ的方程，解得λ值 ，即得向量c的坐标
试题解析：解：(1) ∵ a·b＝2n－2，|a|＝
，|b|＝
，
∴ cos 45°＝
＝
，
∴ 3n2－16n－12＝0(n>1)，
∴ n＝6或n＝－
(舍去)，∴ b＝(－2，6)．
(2) 由(1)知，a·b＝10，|a|2＝5.
∵ c与b同向，故可设c＝λb(λ>0)．
∵ a与c－a垂直，∴ (c－a)·a＝0，
∴ λb·a－|a|2＝0，∴ λ＝
＝
＝
.
∴ c＝
b＝(－1，3)．
步步高达标卷系列答案科目：高中数学 来源： 题型：
【题目】学校为了了解高一新生男生得到体能状况，从高一新生中抽取若干名男生进行铅球测试，把所得数据（精确到0.1米）进行整理后，分成6组画出频率分布直方图的一部分（如下图），已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30，第6小组的频数是7.
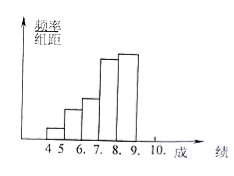
（1）请将频率分布直方图补充完整；
（2）该校参加这次铅球测试的男生有多少人？
（3）若成绩在8.0米以上（含8.0米）的为合格，试求这次铅球测试的成绩的合格率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系
中，直线
的参数方程为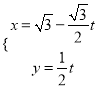
（
为参数），以原点为极点， 
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程为
．
（1）写出曲线
的直角坐标方程；
（2）已知直线
与
轴的交点为
，与曲线
的交点为
， 
，若
的中点为
，求
的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA上的点，且满足
．
(1)求证：四边形EFGH是梯形；
(2)若BD＝a，求梯形EFGH的中位线的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知A(4，－3)，B(2，－1)和直线l：4x＋3y－2＝0．
（1）求在直角坐标平面内满足|PA|＝|PB|的点P的方程；
（2）求在直角坐标平面内一点P满足|PA|＝|PB|且点P到直线l的距离为2的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1，在高为2的梯形
中， 
， 
， 
，过
、
分别作
， 
，垂足分别为
、
。已知
，将梯形
沿
、
同侧折起，得空间几何体
，如图2。
（1）若
，证明： 
；
（2）若
，证明： 
；
（3）在（1），（2）的条件下，求三棱锥
的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
