
已知命题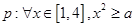 ,命题
,命题 若命“
若命“ ”是真命题,则实数
”是真命题,则实数 的取值范围为 .
的取值范围为 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| ma-nb | m-n |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| ma-nb |
| m-n |
查看答案和解析>>
科目:高中数学 来源:《第2章 推理与证明》2010年单元测试卷(解析版) 题型:解答题
 ”.现已知数列{bn}(bn>0,n∈N+)为等比数列,且bm=a,bn=b(m≠n,m,n∈N+).
”.现已知数列{bn}(bn>0,n∈N+)为等比数列,且bm=a,bn=b(m≠n,m,n∈N+).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com