
【题目】已知集合![]() 是满足下列性质的函数
是满足下列性质的函数![]() 的全体:在定义域
的全体:在定义域![]() 内存在实数
内存在实数![]() ,使得
,使得![]() 成立.
成立.
(1)已知函数![]() ,判断 函数
,判断 函数![]() 是否属于集合
是否属于集合![]() ;
;
(2)若函数![]() 属于集合
属于集合![]() ,试求实数
,试求实数![]() 的取值范围;
的取值范围;
(3) 证明函数![]() 属于集合
属于集合![]() .
.
科目:高中数学 来源: 题型:
【题目】酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL血液中酒精含量低于20mg的驾驶员可以驾驶汽车,酒精含量达到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过几个小时才能驾驶汽车?( )(参考数据:lg0.2≈﹣0.7,1g0.3≈﹣0.5,1g0.7≈﹣0.15,1g0.8≈﹣0.1)
A.1B.3C.5D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面a内作菱形ABCD,边长为1,∠BAD=60°,再在a的上方,分别以△ABD与△CBD为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.

(1)求二面角P-BD-Q的余弦值;
(2)求点P到平面QBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有如下四个命题:
①甲乙两组数据分别为甲:28,31,39,42,45,55,57,58,66;乙:29,34,35,48,42,46,55,53,55,67.则甲乙的中位数分别为45和44.
②相关系数![]() ,表明两个变量的相关性较弱.
,表明两个变量的相关性较弱.
③若由一个2![]() 2列联表中的数据计算得
2列联表中的数据计算得![]() 的观测值
的观测值![]() ,那么有95%的把握认为两个变量有关.
,那么有95%的把握认为两个变量有关.
④用最小二乘法求出一组数据![]() 的回归直线方程
的回归直线方程![]() 后要进行残差分析,相应于数据
后要进行残差分析,相应于数据![]() 的残差是指
的残差是指![]() .
.
以上命题“错误”的序号是_________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]在平面坐标系中xOy中,已知直线l的参考方程为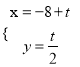 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为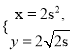 (s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
(s为参数)。设p为曲线C上的动点,求点P到直线l的距离的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了积极支持雄安新区建设,鼓励更多优秀大学生毕业后能到新区去,某985高校组织了一次模拟招聘活动,现从考试成绩中随机抽取100名学生的笔试成绩,并按成绩分成五组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示,(由于某种原因,部分直方图不够清晰),同时规定成绩不低于90分为“优秀”,成绩低于90分为“良好”,且只有成绩“优秀”的学生才能获得专题测试资格.
,得到的频率分布直方图如图所示,(由于某种原因,部分直方图不够清晰),同时规定成绩不低于90分为“优秀”,成绩低于90分为“良好”,且只有成绩“优秀”的学生才能获得专题测试资格.

(1)若已知分数段![]() 与
与![]() 的人数比为2:1,请补全损坏的直方图;
的人数比为2:1,请补全损坏的直方图;
(2)如果用分层抽样的方法从成绩为“优秀”和“良好”中选出10人,设甲是选出的成绩“优秀”中的一个,若从选出的成绩“优秀”的学生中再任选2人参加两项不同的专题测试(每人参加一种,二者互不相同),求甲被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com