Question

6．已知函数f（x）=（a-2）x-ax³在区间[-1，1]上的最大值为2，则a的取值范围是（　　）

• A． [2，10]
• B． [-1，8]
• C． [-2，2]
• D． [0，9]

Answer 1

分析 由函数f（x）=（a-2）x-ax³在区间[-1，1]上的最大值为2，由函数解析式先求其导函数，进而可判断函数在区间[-1，1]上的单调性，从而可求函数的最大值，即可求出a的范围．

解答 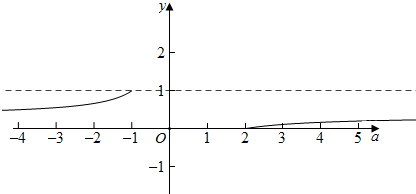解∵f（x）=（a-2）x-ax³，
∴f′（x）=（a-2）-3ax²，
当-1≤a≤2，f′（x）＜0在[-1，1]恒成立，
∴f（x）在[-1，1]上为减函数，
∴f（x）_max=f（-1）=（a-2）×（-1）-a（-1）³=2-a+a=2，满足题意，
当a＜-1，或a＞2时，
令f′（x）=（a-2）-3ax²=0，解得x=±$\sqrt{\frac{a-2}{3a}}$
设y=$\frac{a-2}{3a}$，如图
由图象可得0＜y＜1，
∴$\sqrt{\frac{a-2}{3a}}$＜1，-$\sqrt{\frac{a-2}{3a}}$＞-1，
当a＜-1时，f（x）在[-1，-$\sqrt{\frac{a-2}{3a}}$）和（$\sqrt{\frac{a-2}{3a}}$，1]上单调递增，在（$\sqrt{\frac{a-2}{3a}}$，$\sqrt{\frac{a-2}{3a}}$）单调递减，
故当x=-$\sqrt{\frac{a-2}{3a}}$取得极大值，
则f（-$\sqrt{\frac{a-2}{3a}}$）≤2，
即（a-2）（-$\sqrt{\frac{a-2}{3a}}$）-a（-$\sqrt{\frac{a-2}{3a}}$）³≤2，
即（a-2）³-27a≥0，
当a＞2时，f（x）在[-1，-$\sqrt{\frac{a-2}{3a}}$）和（$\sqrt{\frac{a-2}{3a}}$，1]上单调递减，在（$\sqrt{\frac{a-2}{3a}}$，$\sqrt{\frac{a-2}{3a}}$）单调递增，
故当x=$\sqrt{\frac{a-2}{3a}}$取得极大值，
则f（$\sqrt{\frac{a-2}{3a}}$）≤2，
即（a-2）$\sqrt{\frac{a-2}{3a}}$-a（$\sqrt{\frac{a-2}{3a}}$）³≤2，
即（a-2）³-27a≤0，
设g（a）=（a-2）³-27a，并画出图象，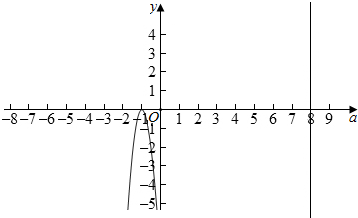

由图象可知，
当2＜a≤8时，满足题意，
综上所述：a的取值范为[-1，8]，
故选：B．

点评 此题考查了利用导数求函数的单调区间，还考查了学生在函数字母的不等式分类讨论思想及学生的计算能力，属于难题．