
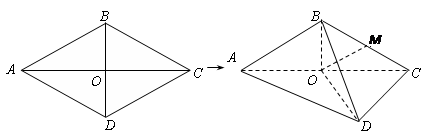
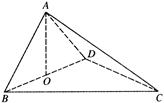
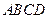 的边长为
的边长为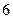 ,
,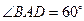 ,
,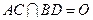 .将菱形
.将菱形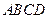 沿对角线
沿对角线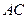 折起,使
折起,使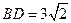 ,得到三棱锥
,得到三棱锥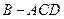 .
.
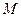 是棱
是棱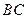 的中点,求证:
的中点,求证: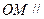 平面
平面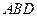 ;
;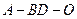 的余弦值;
的余弦值; 是线段
是线段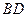 上一个动点,试确定
上一个动点,试确定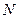 点的位置,使得
点的位置,使得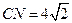 ,并证明你的结论.
,并证明你的结论. 是菱形
是菱形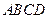 的对角线的交点,
的对角线的交点,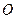 是
是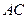 的中点.又点
的中点.又点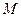 是棱
是棱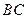 的中点,
的中点,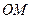 是
是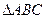 的中位线,
的中位线,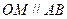 . ………………1分
. ………………1分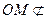 平面
平面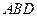 ,
,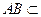 平面
平面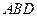 ,
,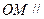 平面
平面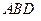 . ………………3分
. ………………3分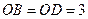 ,
,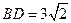 ,
,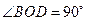 ,
,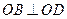 . ………………4分
. ………………4分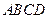 ,所以
,所以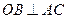 ,
,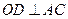 .
. ,如图所示.
,如图所示.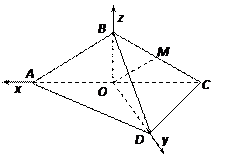
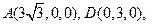
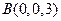 .
.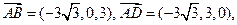 ………………6分
………………6分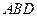 的法向量为
的法向量为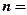
 ,
,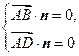 即:
即: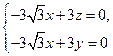
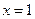 ,则
,则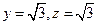 ,所以
,所以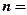
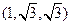 . ………………7分
. ………………7分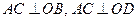 ,所以
,所以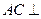 平面
平面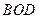 .
. 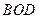 的法向量与
的法向量与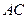 平行,
平行,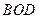 的法向量为
的法向量为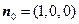 . ………………8分
. ………………8分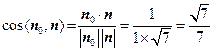 ,
,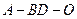 是锐角,
是锐角,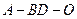 的余弦值为
的余弦值为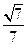 . ……………9分
. ……………9分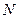 是线段
是线段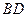 上一个动点,设
上一个动点,设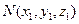 ,
,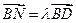 ,
,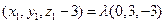 ,
,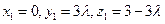 , ……………10分
, ……………10分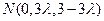 ,
,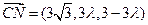 ,
,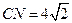 得
得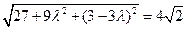 ,即
,即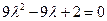 ,…………11分
,…………11分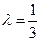 或
或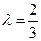 , ……………12分
, ……………12分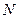 点的坐标为
点的坐标为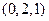 或
或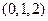 . ……………13分
. ……………13分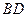 的三等分点,
的三等分点,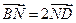 或
或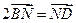 )
)

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源:不详 题型:解答题
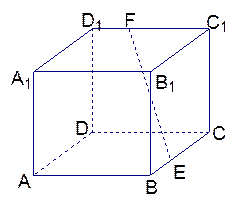
 边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

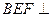 平
平 面DEF;
面DEF; 角A—BF—E的大小。
角A—BF—E的大小。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com