练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
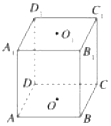
    14．如图所示，在正方体ABCD-A1B1C1D1中，O1、O为上、下底面的中心，在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条．

    分析 DD1与平面AB1C相交；由A1D∥B1C，知A1D∥平面AB1C；A1D1与平面AB1C相交；C1D1与平面AB1C相交；由O1D∥OB1，知O1D∥平面AB1C．

    解答 解：在正方体ABCD-A1B1C1D1中，O1、O为上、下底面的中心，
    ∵DD1∥BB1，BB1∩平面AB1C=B1，
    ∴DD1与平面AB1C相交；
    ∵A1D∥B1C，AD1?平面AB1C，B1C?平面AB1C，∴A1D∥平面AB1C；
    A1D1∥B1C1，B1C1∩平面AB1C=B1，
    ∴A1D1与平面AB1C相交；
    ∵C1D1∥A1B1，A1B1∩平面AB1C=B1，
    ∴C1D1与平面AB1C相交；
    ∵O1D∥OB1，OB1?平面AB1C，
    ∴O1D∥平面AB1C．
    ∴在直线D1D、A1D、A1D1、C1D1、O1D与平面AB1C平行的直线有2条．
    故答案为：2．

    点评 本题考查直线与平行的位置关系的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

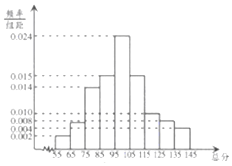    12．从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本，分别统计出这些试卷总分，由总分得到如下的频率分布直方图．
    （1）求这100份数学试卷的样本平均分$\overline x$和样本方差s2
    （同一组中的数据用该组区间的中点值作代表）
    （2）由直方图可以认为，这批学生的数学总分Z服从正态分布N（μ，σ2），其中μ近似为样本平均数$\overline x$，σ2近似为样本方差s2．
    ①利用该正态分布，求P（81＜z＜119）；
    ②记X表示2400名学生的数学总分位于区间（81，119）的人数，利用①的结果，求EX（用样本的分布区估计总体的分布）．
    附：$\sqrt{366}$≈19，$\sqrt{326}$≈18，若Z=～N（μ，2），则P（μ-σ2），则P（μ-σ＜Z＜μ+σ）=0.6826，P（μ-2σ＜Z＜μ+2σ）=0.9544．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的短半轴长为1，离心率为$\frac{\sqrt{3}}{2}$
    （1）求椭圆C的方程
    （2）直线l与椭圆C有唯一公共点M，设直线l的斜率为k，M在椭圆C上移动时，作OH⊥l于H（O为坐标原点），当|OH|=$\frac{4}{5}$|OM|时，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知数列{an}满足a2=$\frac{7}{2}$，且an+1=3an-1（n∈N*）．
    （1）求数列{an}的通项公式以及数列{an}的前n项和Sn的表达式；
    （2）若不等式$\frac{{a}_{n}+\frac{1}{2}}{{a}_{n+1}-\frac{3}{2}}$≤m对?n∈N*恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．数轴上有四个间隔为1的点依次记为A、B、C、D，在线段AD上随机取一点E，则E点到B、C两点的距离之和小于2的概率为$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设命题 p：?n∈N，3n≥n2+1，则￢p为（　　）
    A．?n∈N，3n＜n2+1B．$?{n_0}∈N，{3^{n_0}}＜n_0^2+1$
    C．?n∈N，3n≤n2+1D．$?{n_0}∈N，{3^{n_0}}≥n_0^2+1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．抛物线 M：y2=2px（p＞0）与椭圆 $N：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$有相同的焦点F，抛物线M与 椭圆N交于A，B，若F，A，B共线，则椭圆N的离心率等于$\sqrt{2}$-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．以下说法正确的有②④
    ①若p：?x0∈R，x${\;}_{0}^{2}$-x0＞0，则￢p：?x∈R，x2-x＞0
    ②已知m，n是两条不同的直线，α，β是两个不同是平面，若m⊥α，m∥n，n∥β，则α⊥β
    ③“m＞2”是“?k∈R，y=kx+2k与x2+y2+mx=0都有公共点”的充分不必要条件
    ④在△ABC中，AB=AC=3，BC=2，p是△ABC内部的一点，若$\frac{{S}_{△PAB}}{\overrightarrow{PA}•\overrightarrow{PB}}$=$\frac{{S}_{△PBC}}{\overrightarrow{PB}•\overrightarrow{PC}}$=$\frac{{S}_{△PAC}}{\overrightarrow{PA}•\overrightarrow{PC}}$（S△PAB，S△PBC，S△PAC表示相应三角形的面积），则PA+PB+PC=2$\sqrt{2}$+$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．在△ABC中，a、b、c分别为A、B、C所对的边，且2acosB+bcosA=2c，则△ABC是（　　）
    A．锐角三角形B．钝角三角形C．直角三角形D．斜三角形

    查看答案和解析>>

    同步练习册答案