
【题目】已知函数f(x)=(x﹣1)2+a(lnx﹣x+1)(其中a∈R,且a为常数)
(1)若对于任意的x∈(1,+∞),都有f(x)>0成立,求a的取值范围;
(2)在(1)的条件下,若方程f(x)+a+1=0在x∈(0,2]上有且只有一个实根,求a的取值范围.
【答案】解:(1)∵f(x)=(x﹣1)2+a(lnx﹣x+1),
∴f′(x)=2(x﹣1)+a(![]() ﹣1)=(x﹣1)(2﹣
﹣1)=(x﹣1)(2﹣![]() );
);
且f(1)=0+a(ln1﹣1+1)=0,
①当a≤2时,f′(x)>0在(1,+∞)上恒成立,
故f(x)>=f(1)=0;
②当a>2时,
可知f(x)在(1,![]() )上是减函数,在(
)上是减函数,在(![]() ,+∞)上是增函数;
,+∞)上是增函数;
故f(![]() )<0;
)<0;
综上所述,a≤2;
(2)f(x)+a+1=(x﹣1)2+a(lnx﹣x+1)+a+1,
当a<0时,f(x)+a+1在(0,1]上是减函数,在(1,2]上是增函数;
且![]() ((x﹣1)2+a(lnx﹣x+1)+a+1)=+∞,
((x﹣1)2+a(lnx﹣x+1)+a+1)=+∞,
f(1)+a+1=a+1,f(2)+a+1=1+a(ln2﹣1)+a+1;
故a+1=0或1+a(ln2﹣1)+a+1<0;
故a=﹣1或a<﹣![]() ;
;
当a=0时,f(x)+a+1=(x﹣1)2+1>0,故不成立;
当0<a<2时,
f(x)+a+1在(0,![]() ]上是增函数,在(
]上是增函数,在(![]() ,1]上是减函数,在(1,2]上是增函数;
,1]上是减函数,在(1,2]上是增函数;
且![]() ((x﹣1)2+a(lnx﹣x+1)+a+1)=﹣∞,
((x﹣1)2+a(lnx﹣x+1)+a+1)=﹣∞,
f(1)+a+1=a+1>0,
故方程f(x)+a+1=0在x∈(0,2]上有且只有一个实根,
当a=2时,f(x)+a+1=(x﹣1)2+2(lnx﹣x+1)+2+1=(x﹣1)2+2(lnx﹣x+1)+3,
故f(x)在(0,2]上是增函数;
且![]() ((x﹣1)2+2(lnx﹣x+1)+3)=﹣∞,f(1)=3>0;
((x﹣1)2+2(lnx﹣x+1)+3)=﹣∞,f(1)=3>0;
故方程f(x)+a+1=0在x∈(0,2]上有且只有一个实根,
综上所述,a<﹣![]() 或a=﹣1或0<a≤2.
或a=﹣1或0<a≤2.
【解析】(1)求导f′(x)=2(x﹣1)+a(![]() ﹣1)=(x﹣1)(2﹣
﹣1)=(x﹣1)(2﹣![]() ),且f(1)=0+a(ln1﹣1+1)=0,从而讨论以确定函数的单调性,从而解得;
),且f(1)=0+a(ln1﹣1+1)=0,从而讨论以确定函数的单调性,从而解得;
(2)化简f(x)+a+1=(x﹣1)2+a(lnx﹣x+1)+a+1,从而讨论以确定函数的单调性,从而解得.
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识,掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】圆x2+y2+2x﹣4y﹣6=0的圆心和半径分别是( )
A.(﹣1,﹣2),11
B.(﹣1,2),11
C.(﹣1,﹣2), ![]()
D.(﹣1,2), ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知可导函数y=f(x)在点P(x0 , f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)﹣g(x),则( )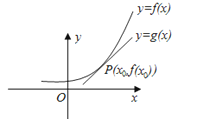
A.F′(x0)=0,x=x0是F(x)的极大值点
B.F′(x0)=0,x=x0是F(x)的极小值点
C.F′(x0)≠0,x=x0不是F(x)的极值点
D.F′(x0)≠0,x=x0是F(x)的极值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1 , 底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
(1)求![]() 的长;
的长;
(2)求cos(![]()
![]() )的值;
)的值;
(3)求证A1B⊥C1M.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+α)(A>0,ω>0,0<α<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为 . 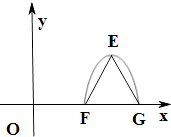
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
. 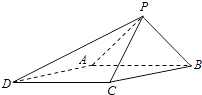
(1)求证:AB⊥PC;
(2)求二面角B一PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A(1,1),B(2,0),| ![]() |=1.
|=1.
(1)求 ![]() 与
与 ![]() 夹角;
夹角;
(2)若 ![]() 与
与 ![]() 垂直,求点C的坐标;
垂直,求点C的坐标;
(3)求| ![]() +
+ ![]() +
+ ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com