6名同学随意站成一排,求下列各种情况发生的概率:
(1)甲站左端;
(2)甲站左端,乙站右端;
(3)甲、乙两人相邻;
(4)甲、乙两人不相邻;
(5)甲不站排头、排尾;
(6)甲站在乙的左边(可以相邻,也可以不相邻).
解:(1)题目要求甲站在左端,
先排列甲,余下的五个人在五个位置全排列,
共有A
55=120种结果.
(2)题目要求甲站左端,乙站右端;
甲和乙站好之后,余下的四个元素在四个位置进行全排列,
共有A
44=24种结果,
(3)甲、乙两人相邻,则可以采用捆绑法,
把甲和乙看做一个元素,同其他四个元素进行排列,甲和乙内部还有一个排列,
共有A
55A
22=240种结果.
(4)甲、乙两人不相邻,则可以采用插空法,
先把其他四个人在四个位置排列,四个人形成五个空,
使甲和乙在这五个空上选两个位置排列,
共有A
44A
52=480种结果.
(5)题目要求甲不站排头、排尾,可以先排有限制条件的元素,
甲不在两端,则甲可以在中间四个位置选一个进行排列,
余下的五个人在五个位置全排列,
共有A
41A
55=480种结果
(6)6个人在6个位置全排列,
∵甲在乙的左边和右边的概率是一样的,
∴甲站在乙的左边有
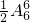
=360种结果.
分析:(1)题目要求甲站在左端,先排列甲,余下的五个人在五个位置全排列,用排列数写出结果.
(2)题目要求甲站左端,乙站右端,甲和乙站好之后,余下的四个元素在四个位置进行全排列.
(3)甲、乙两人相邻,则可以采用捆绑法,把甲和乙看做一个元素,同其他四个元素进行排列,甲和乙内部还有一个排列.
(4)甲、乙两人不相邻,则可以采用插空法,先把其他四个人在四个位置排列,四个人形成五个空,使甲和乙在这五个空上选两个位置排列.
(5)题目要求甲不站排头、排尾,可以先排有限制条件的元素,甲不在两端,则甲可以在中间四个位置选一个进行排列,余下的五个人在五个位置全排列.
(6)6个人在6个位置全排列,甲在乙的左边和右边的概率是一样的,把六个人全排列得到的结果数处于2即可.
点评:站队问题是排列组合中的典型问题,解题时要先排限制条件多的元素,把限制条件比较多的元素排列后,再排没有限制条件的元素,最后要用分步计数原理得到结果.

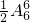 =360种结果.
=360种结果.

 阅读快车系列答案
阅读快车系列答案