
分析 (1)求出函数的导数,通过m的范围,求解函数的单调性.
(2)利用不等式转化函数的单调性,构造函数通过导数,求解证明即可.
解答 解:(1)$f'(x)=\frac{1}{x}-m=\frac{1-mx}{x}$
当m≤0时,f'(x)≥0,∴f(x)在(0,+∈)是增函数.
当m>0时,f(x)在(0,$\frac{1}{m}$)是增函数,($\frac{1}{m}$,+∞)是减函数.
(2)对任意的$0<{x_1}<{x_2},\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}<\frac{1}{x_1}$,
可变形为$\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}<\frac{1}{x_1}?ln{x_2}-ln{x_1}<\frac{{{x_2}-{x_1}}}{x_1}=\frac{x_2}{x_1}-1$$?ln\frac{x_2}{x_1}<\frac{x_2}{x_1}-1?lnt<r-1(t=\frac{x_2}{x_1}>1)$,
令φ(t)=lnt-t+1,$φ'(t)=\frac{1}{t}-1<0$,
∴φ(t)在(1,+∞)单调递减,
∴φ(t)<φ(1)=0.
点评 本题考查函数的导数的应用,考查转化思想以及计算能力.考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
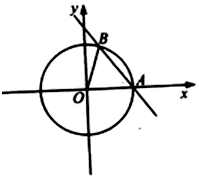 已知:如图所示,直线AB:$\sqrt{3}x+y-2\sqrt{3}=0$与圆O:x2+y2=4相交于点A,B,求证:△AOB是等边三角形.
已知:如图所示,直线AB:$\sqrt{3}x+y-2\sqrt{3}=0$与圆O:x2+y2=4相交于点A,B,求证:△AOB是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com