
【题目】甲、乙二人同时从![]() 地赶住
地赶住![]() 地,甲先骑自行车到两地的中点再改为跑步;乙先跑步到两地的中点再改为骑自行车,最后两人同时到达
地,甲先骑自行车到两地的中点再改为跑步;乙先跑步到两地的中点再改为骑自行车,最后两人同时到达![]() 地.已知甲骑自行车比乙骑自行车的速度快,且两人骑车的速度均大于跑步的速度.现将两人离开
地.已知甲骑自行车比乙骑自行车的速度快,且两人骑车的速度均大于跑步的速度.现将两人离开![]() 地的距离
地的距离![]() 与所用时间
与所用时间![]() 的函数关系用图象表示如下:
的函数关系用图象表示如下:

则上述四个函数图象中,甲、乙两人运行的函数关系的图象应该分别是( )
A. 图①、图② B. 图①、图④ C. 图③、图② D. 图③、图④
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 为抛物线
为抛物线![]() 上不同的两点,
上不同的两点, ![]() 分别是抛物线
分别是抛物线![]() 在点
在点![]() 、点
、点![]() 处的切线,
处的切线, ![]() 是
是![]() 的交点.
的交点.
(1)当直线![]() 经过焦点
经过焦点![]() 时,求证:点
时,求证:点![]() 在定直线上;
在定直线上;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:

(1)求高三(1)班全体女生的人数;
(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)之间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析女生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为![]() ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
如图,在阳马![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 为
为![]() 中点,点
中点,点![]() 在
在![]() 上,且
上,且![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() .
.
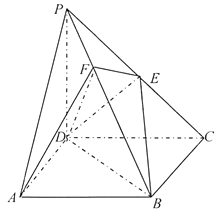
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)试判断四面体![]() 是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;
(Ⅲ)已知![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() .
.
(1)求函数![]() 在
在![]() 上的单调区间,并给以证明;
上的单调区间,并给以证明;
(2)设关于![]() 的方程
的方程![]() 的两根为
的两根为![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意的
对任意的![]() 及
及![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com