【答案】
分析:(Ⅰ)先利用函数的单调性求出前三个函数的最小值,代入x
3+ax
2+bx+c=0可得a
2=2b+3.
(Ⅱ)x
1,x
2是方程f'(x)=3x
2+2ax+b=0的根⇒有
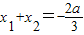
,
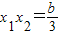
△=(2a)
2-12b>0,得b<3
①利用两根之差的绝对值和两根之和,两根之积的关系,可以求得a,b,c,即得.
②|M-N|的取值即为两函数值之间的关系,利用根与系数的关系进行转化,在利用所求b<3或a<-1代入即可.
解答:解:(Ⅰ)三个函数的最小值依次为1,
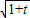
,
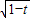
,(3分)
由f(1)=0,得c=-a-b-1
∴f(x)=x
3+ax
2+bx+c=x
3+ax
2+bx-(a+b+1)=(x-1)[x
2+(a+1)x+(a+b+1)],
故方程x
2+(a+1)x+(a+b+1)=0的两根是
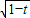
,
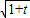
.
故
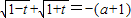
,
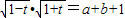
.(4分)
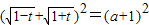
,即2+2(a+b+1)=(a+1)
2∴a
2=2b+3.(5分)
(Ⅱ)①依题意x
1,x
2是方程f'(x)=3x
2+2ax+b=0的根,
故有
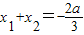
,
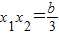
,
且△=(2a)
2-12b>0,得b<3.
由
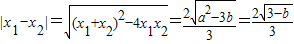
(7分)
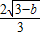
=

;得,b=2,a
2=2b+3=7.
由(Ⅰ)知
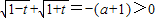
,故a<-1,
∴
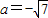
,
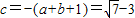
∴
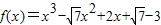
.(9分)
②|M-N|=|f(x
1)-f(x
2)|
=|(x
13-x
23)+a(x
12-x
22)+b(x
1-x
2)|
=|x
1-x
2|•|(x
1+x
2)
2-x
1x
2+a(x
1+x
2)+b|
=
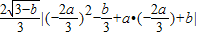
=
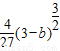
(或
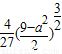
).(11分)
由(Ⅰ)
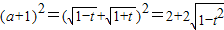
∵0<t<1,∴2<(a+1)
2<4,
又a<-1,
∴
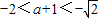
,
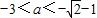
,
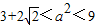
(或
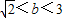
)(13分)
∴
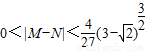
.(15分)
点评:函数的极值表示函数在某一点附近的情况,是在局部上对函数值的比较;函数的最值表示函数在一个区间上的情况,是对函数在整个区间上的函数值的比较.函数的极值不一定是最值,函数的最值也不一定是极值.

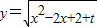 ,
,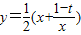 (x>0)的最小值恰好是方程x3+ax2+bx+c=0的三个根,其中0<t<1.
(x>0)的最小值恰好是方程x3+ax2+bx+c=0的三个根,其中0<t<1.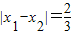 ,求函数f(x)的解析式;
,求函数f(x)的解析式;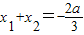 ,
,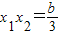 △=(2a)2-12b>0,得b<3
△=(2a)2-12b>0,得b<3 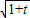 ,
,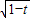 ,(3分)
,(3分)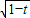 ,
,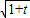 .
.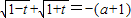 ,
,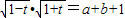 .(4分)
.(4分)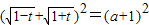 ,即2+2(a+b+1)=(a+1)2
,即2+2(a+b+1)=(a+1)2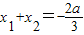 ,
,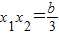 ,
,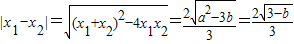 (7分)
(7分)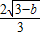 =
= ;得,b=2,a2=2b+3=7.
;得,b=2,a2=2b+3=7.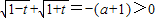 ,故a<-1,
,故a<-1,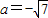 ,
,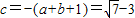
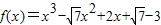 .(9分)
.(9分)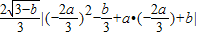
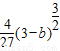 (或
(或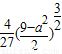 ).(11分)
).(11分)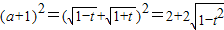
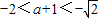 ,
,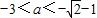 ,
,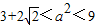 (或
(或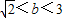 )(13分)
)(13分)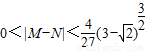 .(15分)
.(15分)

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案