
下列说法中
①设定点 ,
,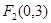 ,动点
,动点 满足条件
满足条件 ,则动点
,则动点 的轨迹是椭圆或线段;
的轨迹是椭圆或线段;
②命题“每个指数函数都是单调函数”是全称命题,而且是真命题.
③离心率为 长轴长为8的椭圆标准方程为
长轴长为8的椭圆标准方程为 ;
;
④若 ,则二次曲线
,则二次曲线 的焦点坐标是(±1,0).
的焦点坐标是(±1,0).
其中正确的为 (写出所有真命题的序号)
②④
解析试题分析:①设定点 ,
,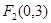 ,动点
,动点 满足条件
满足条件 ,则动点
,则动点 的轨迹是椭圆或线段,不对,应有无轨迹的情况。
的轨迹是椭圆或线段,不对,应有无轨迹的情况。
②命题“每个指数函数都是单调函数”是全称命题,而且是真命题.结合全称命题的定义知其正确。
③离心率为 长轴长为8的椭圆标准方程为
长轴长为8的椭圆标准方程为 ,不正确,因为由
,不正确,因为由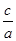 =
= 2a=8,得a=4,c=2,
2a=8,得a=4,c=2,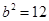 ,根据焦点所在坐标轴不同,应有两种形式。
,根据焦点所在坐标轴不同,应有两种形式。
④若 ,则二次曲线
,则二次曲线 的焦点坐标是(±1,0),正确,因为
的焦点坐标是(±1,0),正确,因为 时,
时, 表示焦点在x轴的双曲线,且
表示焦点在x轴的双曲线,且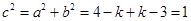 。
。
故答案为②④。
考点:本题主要考查命题的概念,椭圆、双曲线的标准方程及其几何性质。
点评:中档题,本题通过判断几个命题的真假,综合考查了全称命题、特称命题、椭圆和的标准方程、几何性质等,对考查学生灵活运用数学知识解题的能力有较好的考查。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
| x2 |
| 4-k |
| y2 |
| 3-k |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
| x2 |
| 4-k |
| y2 |
| 3-k |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| lgx |
| 3 |
| π |
| 6 |
| x2 |
| 25 |
| y2 |
| 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| p |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| θ |
| 2 |
| 1 |
| |AF| |
| 1 |
| p |
| 1 |
| |BF| |
查看答案和解析>>
科目:高中数学 来源:2014届四川省高二5月月考考理科数学试卷(解析版) 题型:填空题
下列说法中,正确的有 .
①若点 是抛物线
是抛物线 上一点,则该点到抛物线的焦点的距离是
上一点,则该点到抛物线的焦点的距离是 ;
;
②设 、
、 为双曲线
为双曲线 的两个焦点,
的两个焦点, 为双曲线上一动点,
为双曲线上一动点, ,则
,则 的面积为
的面积为 ;
;
③设定圆 上有一动点
上有一动点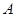 ,圆
,圆 内一定点
内一定点 ,
, 的垂直平分线与半径
的垂直平分线与半径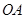 的交点为点
的交点为点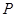 ,则
,则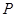 的轨迹为一椭圆;
的轨迹为一椭圆;
④设抛物线焦点到准线的距离为 ,过抛物线焦点
,过抛物线焦点 的直线交抛物线于A、B两点,则
的直线交抛物线于A、B两点,则 、
、 、
、 成等差数列.
成等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com