
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 在
在![]() 上单调递减,试求
上单调递减,试求![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 的最小值为
的最小值为![]() ,试求
,试求![]() 的值.
的值.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .(Ⅲ)
.(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)利用导数求出![]() 处的切线斜率,根据点斜式写出切线方程;(Ⅱ)函数
处的切线斜率,根据点斜式写出切线方程;(Ⅱ)函数![]() 在
在![]() 上单调递减,即当
上单调递减,即当![]() 时,
时, ![]() 恒成立,等价于
恒成立,等价于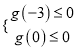 ,即可求出
,即可求出![]() 的取值范围;(Ⅲ)根据函数的单调性,得出函数
的取值范围;(Ⅲ)根据函数的单调性,得出函数![]() 的最小值只能在
的最小值只能在![]() 处取得,从而求得
处取得,从而求得![]() 的值.
的值.
试题解析:(Ⅰ)当![]() 时,由
时,由![]() 得:
得: ![]() .
.
又∵![]()
∴![]() .
.
∴切线方程为: ![]() ,即
,即![]() .
.
(Ⅱ)∵函数![]() 在
在![]() 上单调递减
上单调递减
∴当![]() 时,
时, ![]() 恒成立,即当
恒成立,即当![]() 时,
时, ![]() 恒成立.
恒成立.
∵函数![]() 的对称轴为
的对称轴为![]() ,并且开口向上,
,并且开口向上,
∴当![]() 时,函数
时,函数![]() 单调递减;当
单调递减;当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
∴“当![]() 时,
时, ![]() 恒成立”必须满足:
恒成立”必须满足: 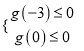 ,解得
,解得![]() .
.
∴![]() ,
, ![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)设![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 恒成立,
恒成立,
∴![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调递增,函数
上单调递增,函数![]() 没有最小值.
没有最小值.
②当![]() 时,
时, ![]() .
.
令![]() 得:
得: ![]() ,解得
,解得![]() .
.
∴当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
∴当![]() 时,
时, ![]() 取得极大值;
取得极大值;
当![]() 时,
时, ![]() 取得极小值.
取得极小值.
∴当![]() 时,
时, ![]() ,
,
∴![]() ,则
,则![]() ,
,
又∵函数![]() 的最小值为
的最小值为![]() ,
,
∴函数![]() 的最小值只能在
的最小值只能在![]() 处取得,则
处取得,则![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.


科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域内的每一个值
对定义域内的每一个值![]() ,在其定义域内都存在唯一的
,在其定义域内都存在唯一的![]() ,使
,使![]() 成立,则称该函数为“
成立,则称该函数为“![]() 函数”.
函数”.
(1)判断函数![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上是“
上是“![]() 函数”,求
函数”,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“
上为“![]() 函数”.若存在实数
函数”.若存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间,分别从该品牌手机的甲、乙两种型号中各选取![]() 部进行测试,其结果如下:
部进行测试,其结果如下:
甲种手机供电时间(小时) |
|
|
|
|
|
|
乙种手机供电时间(小时) |
|
|
|
|
|
|
(1)求甲、乙两种手机供电时间的平均值与方差,并判断哪种手机电池质量好;
(2)为了进一步研究乙种手机的电池性能,从上述![]() 部乙种手机中随机抽取
部乙种手机中随机抽取![]() 部求这两部手机中恰有一部手机的供电时间大于该种手机供电时间平均值的概率.
部求这两部手机中恰有一部手机的供电时间大于该种手机供电时间平均值的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如图的列联表. 已知在全部105人中随机抽取一人为优秀的概率为![]() .
.

(1)请完成上面的列联表;
(2)根据列联表的数据,若按![]() 的可靠性要求,能否认为“成绩与班级有关系”;
的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到8或9号的概率.
参考公式和数据: ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 到定点
到定点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小1,设动点
的距离小1,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 、
、![]() 两个不同的点,过点
两个不同的点,过点![]() 、
、![]() 分别作曲线
分别作曲线![]() 的切线,且二者相交于点
的切线,且二者相交于点![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)求证: ![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数的值域;
时,求函数的值域;
(2)若函数![]() 的最大值是
的最大值是![]() ,求
,求![]() 的值;
的值;
(3)已知![]() ,若存在两个不同的正数
,若存在两个不同的正数![]() ,当函数
,当函数![]() 的定义域为
的定义域为![]() 时,
时,![]() 的值域为
的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足:①a1=1;②所有项an∈N*;③1=a1<a2<…<an<an+1<….设集合Am={n|an≤m,m∈N*),将集合Am中的元素的最大值记为bm,即bm是数列{an}中满足不等式an≤m的所有项的项数的最大值.我们称数列{bn}为数列{an}的伴随数列.
例如,数列1,3,5的伴随数列为1,1,2,2,3.
(I)若数列{an}的伴随数列为1,1,2,2,2,3,3,3,3……,请写出数列{an};
(II)设an=4n-1,求数列{an}的伴随数列{bn}的前50项之和;
(III)若数列{an}的前n项和![]() (其中c为常数),求数列{an}的伴随数列{bm}的前m项和Tm.
(其中c为常数),求数列{an}的伴随数列{bm}的前m项和Tm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com