
分析 (Ⅰ)若p∧q为真,则p真且q真,将a=1代入,分别解两个不等式(组),再求其交集可得实数x的取值范围;
(Ⅱ)若¬q是¬p的必要不充分条件,即q⇒p为真且p⇒q为假,进而可得实数a的取值范围.
解答 解:(Ⅰ)由x2-4ax+3a2<0,得(x-3a)(x-a)<0,
当a=1时,解得1<x<3,即p为真时实数x的取值范围是1<x<3.
由$\left\{\begin{array}{l}{{x}^{2}-x-6≤0}\\{{x}^{2}+2x-8>0}\end{array}\right.$,得2<x≤3,即q为真时实数x的取值范围是2<x≤3.
若p∧q为真,则p真且q真,所以实数x的取值范围是2<x<3.
(Ⅱ)¬q是¬p的必要不充分条件,即q⇒p为真且p⇒q为假,
设A={x|p(x)},B={x|q(x)},则B?A,
又B=(2,3],
当a>0时,A=(a,3a);
a<0时,A=(3a,a).
所以当a>0时,有$\left\{\begin{array}{l}{a≤2}\\{3<3a}\end{array}\right.$解得1<a≤2;
当a<0时,显然A∩B=∅,不合题意.
综上所述,实数a的取值范围是1<a≤2.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,二次不等式的解法,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:
从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
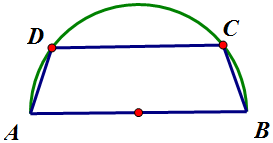 有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.
有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com