
| ��� | ���з���֧����xi�� | ����yi�� |
| 2011 2012 2013 2014 2015 2016 | 5 11 4 5 3 2 | 31 40 30 34 25 20 |
| �ϼ� | 30 | 180 |
���� ��1���������������ݣ�������С���˷���Ҫ��6�����ݣ������ݱ��ƽ�����������ݱ�Ļ��ĺͣ������ƽ���ͣ����빫ʽ���b��ֵ�������a��ֵ��д�����Իع鷽�̣�
��2���оٳ����еĻ����¼�����������������¼��ĸ��������̼��ɣ�
��� �⣺��1������������±���
| ��� | xi | yi | xi•yi | xi2 |
| 1 | 5 | 31 | 155 | 25 |
| 2 | 11 | 40 | 440 | 121 |
| 3 | 4 | 30 | 120 | 16 |
| 4 | 5 | 34 | 170 | 25 |
| 5 | 3 | 25 | 75 | 9 |
| 6 | 2 | 20 | 40 | 4 |
| $\overline{{x}_{i}}$=5 | $\overline{{y}_{i}}$=30 | $\sum_{i=1}^{6}$xi•yi=1000 | $\sum_{i=1}^{6}$xi2=200 |
| ��� | xi | yi | $\widehat{{y}_{i}}$ | �� |
| 1 | 5 | 31 | 30 | 1 |
| 2 | 11 | 40 | 42 | 2 |
| 3 | 4 | 30 | 28 | 2 |
| 4 | 5 | 34 | 30 | 4 |
| 5 | 3 | 25 | 26 | 1 |
| 6 | 2 | 20 | 24 | 4 |
���� ���⿼�����Իع������Ӧ�ã��������Ĺؼ���������С���˷������������Իع鷽�̵�ϵ��������������Ŀ���Եıر�������������һ���е��⣮


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{5}$ | B�� | -$\frac{4}{5}$ | C�� | $\frac{3}{5}$ | D�� | -$\frac{3}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{1}{3}$��1�� | B�� | [$\frac{1}{3}$��1�� | C�� | ��0��$\frac{1}{3}$�� | D�� | ��0��$\frac{1}{3}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
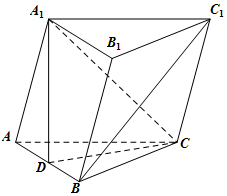 ��ͼ��������ABC-A1B1C1�У�AC=BC��AB=AA1����A1AB=60�㣬D��AB���е㣮
��ͼ��������ABC-A1B1C1�У�AC=BC��AB=AA1����A1AB=60�㣬D��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -3 | C�� | -3i | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
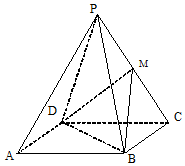 ��֪����P-ABCD�е����ı���ABCD�������Σ������涼�DZ߳�Ϊ2���������Σ�M����PC���е㣮�����ռ�ֱ������ϵ�����ÿռ�������������������⣺
��֪����P-ABCD�е����ı���ABCD�������Σ������涼�DZ߳�Ϊ2���������Σ�M����PC���е㣮�����ռ�ֱ������ϵ�����ÿռ�������������������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
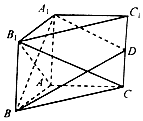 ��ͼ��ʾ��������A1B1C1-ABC�IJ���AA1�͵���ABC��AB��AC��AB=AA1��D����CC1���е㣮
��ͼ��ʾ��������A1B1C1-ABC�IJ���AA1�͵���ABC��AB��AC��AB=AA1��D����CC1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com