
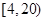 个范围内的学生中随机选2人,求能准确回忆
个范围内的学生中随机选2人,求能准确回忆 个单词至少有一人的概率.
个单词至少有一人的概率.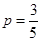 .
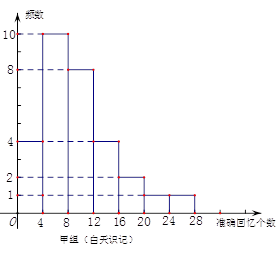
.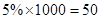 人,由甲组的条形图可知甲组有有:4+10+8+4+2+1+1=30人;故乙组有20人
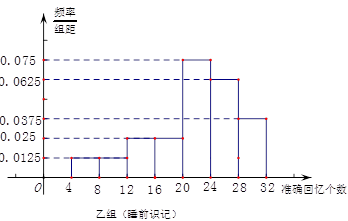
人,由甲组的条形图可知甲组有有:4+10+8+4+2+1+1=30人;故乙组有20人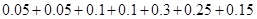 即有1+1+2+2+6+5+3=20人。
即有1+1+2+2+6+5+3=20人。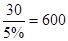 人,“晚上睡前背”的同学有400人。
人,“晚上睡前背”的同学有400人。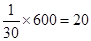 人,“晚上睡前背”的同学有
人,“晚上睡前背”的同学有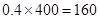 人。
人。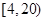 个范围内的学生有6人,能准确回忆
个范围内的学生有6人,能准确回忆 个单词的学生有2人。
个单词的学生有2人。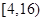 个单词的可能结果有6种,故所求概率为:
个单词的可能结果有6种,故所求概率为: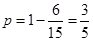
 个单词的可能结果有
个单词的可能结果有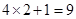 种,故所求概率为:
种,故所求概率为: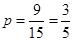


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
| 学历 | 35岁以下 | 35至50岁 | 50岁以上 |
| 本科 | 80 | 30 | 20 |
| 研究生 | x | 20 | y |
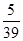 ,求x、y的值.
,求x、y的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组(体重) |  |  | 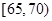 |  |
| 频数(人) |  |  |  |  |
 的频率;
的频率; 中共有几人?
中共有几人? 的人中,任取2人,求体重在
的人中,任取2人,求体重在 中各有1人的概率.
中各有1人的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 名男生和
名男生和 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:| 上网时间(分钟) |  |  |  |  |  |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) |  |  |  |  |  |
| 人数 | 10 | 20 | 40 | 20 | 10 |
 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
 ,其中
,其中
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
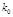 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
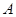 产品过程中记录的产品
产品过程中记录的产品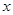 (吨)与相应的生产能耗
(吨)与相应的生产能耗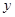 (吨)的几组对应数据,根据表中提供的数据,求出
(吨)的几组对应数据,根据表中提供的数据,求出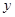 关于
关于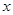 的线性回归方程为
的线性回归方程为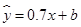 ,那么
,那么 的值为( )
的值为( )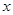 | 3 | 4 | 5 | 6 |
 | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出
只,给每只鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机的捕出 只鱼,记录下其中有记号的鱼的数目,立即放回池塘中。这样的记录做了
只鱼,记录下其中有记号的鱼的数目,立即放回池塘中。这样的记录做了 次,并将记录获取的数据做成以下的茎叶图。
次,并将记录获取的数据做成以下的茎叶图。

 条鱼进行称重,据称重鱼的重量介于
条鱼进行称重,据称重鱼的重量介于 (单位:千克)之间,将测量结果按如下方式分成九组:第一组
(单位:千克)之间,将测量结果按如下方式分成九组:第一组 、第二组
、第二组 ;……,第九组
;……,第九组 。右图是按上述分组方法得到的频率分布直方图的一部分。
。右图是按上述分组方法得到的频率分布直方图的一部分。 千克以上(含
千克以上(含 千克)的条数;
千克)的条数; 的等差数列,请将频率分布直方图补充完整;
的等差数列,请将频率分布直方图补充完整; 只鱼中出现鲤鱼的次数为
只鱼中出现鲤鱼的次数为 ,求
,求 的数学期望。
的数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为 .
.| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 合计 | | | 210 |
 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;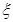 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求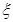 的分布列及数学期望
的分布列及数学期望 .
.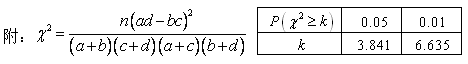
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 环数(环) | 8 | 9 |
| 人数(人) | 7 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com