练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对于函数f（x）=x3cos3（x+ ），下列说法正确的是（ ）
    A.f（x）是奇函数且在（﹣ ， ）上递增
    B.f（x）是奇函数且在（﹣ ， ）上递减
    C.f（x）是偶函数且在（0， ）上递增
    D.f（x）是偶函数且在（0， ）上递减

    【答案】D
    【解析】解：函数f（x）=x3cos3（x+ ）=x3cos（3x+ ）=﹣x3sin3x，
    由于f（﹣x）=﹣x3sin3x=f（x），可知此函数是偶函数，又y=x3与y=sin3x在（ ）上递增，可得f（x）=﹣x3sin3x在（ ）上递减，对照四个选项，D正确，
    故选：D．
    【考点精析】关于本题考查的奇偶性与单调性的综合，需要了解奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某商场将进价为2000元的冰箱以2400元售出，平均每天能售岀8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．

    （1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）

    （2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？

    （3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆E： + =1（a＞b＞0）的两个焦点为F1、F2 ， 且椭圆E过点（0， ），（ ，﹣ ），点A是椭圆上位于第一象限的一点，且△AF1F2的面积S△ = ．
    （1）求点A的坐标；
    （2）过点B（3，0）的直线l与椭圆E相交于点P、Q，直线AP、AQ分别与x轴相交于点M、N，点C（ ，0），证明：|CM||CN|为定值，并求出该定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，设倾斜角为α的直线L： （T为参数）与曲线C： （φ为参数）相交于不同的两点A，B．
    （1）若α= ，若以坐标原点为极点，x轴的正半轴为极轴，求直线AB的极坐标方程；
    （2）若直线的斜率为 ，点P（2， ），求|PA||PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数=

    (1)写出该函数的单调区间;

    (2)若函数=-m恰有3个不同零点,求实数m的取值范围;

    (3)若≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解初三学生女生身高情况，某中学对初三女生身高进行了一次测量，所得数据整理后列出了频率分布表如下：

    组　别

    频数

    频率

    [145.5，149.5）

    1

    0.02

    [149.5，153.5）

    4

    0.08

    [153.5，157.5）

    20

    0.40

    [157.5，161.5）

    15

    0.30

    [161.5，165.5）

    8

    0.16

    [165.5，169.5）

    m

    n

    合　计

    M

    N

    （1）求出表中所表示的数；

    （2）画出频率分布直方图；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，侧棱垂直于底面， ， ， ， ， 分别为， 的中点.

    （1）求证：平面平面；

    （2）求证：在棱上存在一点，使得平面平面；

    （3）求三棱锥的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=是定义在R上的奇函数，且f（1）=1．

    （1）求a，b的值；

    （2）判断并用定义证明f（x）在（+∞）的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知：如图，梯形ABCD中，AD∥BC，∠C= ，以AB为直径的⊙O恰与CD相切于点E，⊙O交BC于F，连结EF．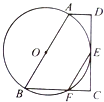

    （1）求证：AD+BC=AB；
    （2）求证：EF是AD与AB的等比中项．

    查看答案和解析>>

    同步练习册答案