【题目】(1)抛掷一颗骰子两次,定义随机变量
试写出随机变量
的分布列(用表格格式);
(2)抛掷一颗骰子两次,在第一次掷得向上一面点数是偶数的条件下,求第二次掷得向上一面点数也是偶数的概率．
小学课时特训系列答案科目：高中数学 来源： 题型：
【题目】节能减排以来，兰州市100户居民的月平均用电量
单位：度
，以
分组的频率分布直方图如图．
求直方图中x的值；
求月平均用电量的众数和中位数；
估计用电量落在
中的概率是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
，且函数g（x）=loga（x2+x+2）（a＞0，且a≠1）在[﹣ 
，1]上的最大值为2，若对任意x1∈[﹣1，2]，存在x2∈[0，3]，使得f（x1）≥g（x2），则实数m的取值范围是（ ）
A.（﹣∞，﹣ 
]
B.（﹣∞， 
]
C.[ ，+∞）
D.[﹣ ，+∞]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将红、黑、蓝、白5张纸牌（其中白纸牌有2张）随机分发给甲、乙、丙、丁4个人，每人至少分得1张，则下列两个事件为互斥事件的是（ ）
A. 事件“甲分得1张白牌”与事件“乙分得1张红牌”
B. 事件“甲分得1张红牌”与事件“乙分得1张蓝牌”
C. 事件“甲分得1张白牌”与事件“乙分得2张白牌”
D. 事件“甲分得2张白牌”与事件“乙分得1张黑牌”
查看答案和解析>>
科目：高中数学 来源： 题型：
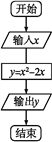
【题目】求函数y=
的值的程序框图如图所示.
(1)指出程序框图中的错误,并写出算法;
(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.
①要使输出的值为正数,输入的x的值应满足什么条件?
②要使输出的值为8,输入的x值应是多少?
③要使输出的y值最小,输入的x值应是多少?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为研究“在n次独立重复试验中,事件A恰好发生k次的概率的和”这个课题，我们可以分三步进行研究：（I）取特殊事件进行研究;(Ⅱ)观察分析上述结果得到研究结论；（Ⅲ）试证明你得到的结论。现在，请你完成:
(1)抛掷硬币4次,设
分别表示正面向上次数为0次,1次,2次,3次,4次的概率,求
(用分数表示),并求
;
(2)抛掷一颗骰子三次,设
分别表示向上一面点数是3恰好出现0次,1次,2次,3次的概率,求
(用分数表示),并求
;
(3)由(1)、(2)写出结论,并对得到的结论给予解释或给予证明.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，四棱锥
，侧面
是边长为2的正三角形，且平面
平面
，底面
是菱形，且
， 
为棱
上的动点，且
.
（1）求证： 
；
（2）试确定
的值，使得二面角
的余弦值为
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，棱柱ABCD-A1B1C1D1中，底面ABCD是平行四边形，侧棱AA1⊥底面ABCD，AB=1，AC=
，BC=BB1=2．
（Ⅰ）求证：AC⊥平面ABB1A1；
（Ⅱ）求点D到平面ABC1的距离d．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
