
(本小题满分14分)设函数 ,
, 的两个极值点为
的两个极值点为 ,线段
,线段 的中点为
的中点为 .
.
(1) 如果函数 为奇函数,求实数
为奇函数,求实数 的值;当
的值;当 时,求函数
时,求函数 图象的对称中心;
图象的对称中心;
(2) 如果 点在第四象限,求实数
点在第四象限,求实数 的范围;
的范围;
(3) 证明:点 也在函数
也在函数 的图象上,且
的图象上,且 为函数
为函数 图象的对称中心.
图象的对称中心.
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
(本小题满分14分)
用总长14.8m的钢条做一个长方体容器的框架,如果所做容器的底面的一边长比另一边长多0.5m,那么高是多少时容器的容积最大?并求出它的最大容积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)已知集合A={a1,a2,a3,a4},B={0,1,2,3},f是从A到B的映射.
(1)若B中每一元素都有原象,这样不同的f有多少个?
(2)若B中的元素0必无原象,这样的f有多少个?
(3)若f满足f(a1)+f(a2)+f(a3)+f(a4)=4,这样的f又有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数 , 其中
, 其中 为常数,且函数
为常数,且函数 图像过原点.
图像过原点.
(1) 求 的值;
的值;
(2) 证明函数 在[0,2]上是单调递增函数;
在[0,2]上是单调递增函数;
(3) 已知函数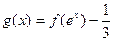 , 求函数
, 求函数 的零点
的零点
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分 分)
分)
已知函数 .(
.( 为常数,
为常数, )
)
(Ⅰ)若 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(Ⅱ)求证:当 时,
时, 在
在 上是增函数;
上是增函数;
(Ⅲ)若对任意的 ,总存在
,总存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com