
【题目】某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为![]() ,高为
,高为![]() ,圆锥的母线长为
,圆锥的母线长为![]() .
.
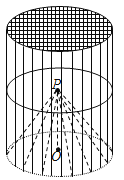
(1)求这种“笼具”的体积(结果精确到0.1![]() );
);
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?
科目:高中数学 来源: 题型:
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每本单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该书每本的成本为![]() 元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: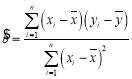
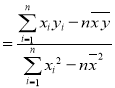 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且![]() 满足:当
满足:当![]() 成立时,总可推出
成立时,总可推出![]() 成立那么下列命题中正确的是( )
成立那么下列命题中正确的是( )
A.若![]() 成立,则当
成立,则当![]() 时均有
时均有![]() 成立
成立
B.若![]() 成立,则当
成立,则当![]() 时均有
时均有![]() 成立
成立
C.若![]() 成立,则当
成立,则当![]() 时均有
时均有![]() 成立
成立
D.若![]() 成立,则当
成立,则当![]() 时均有
时均有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在教材中,我们已研究出如下结论:平面内![]() 条直线最多可将平面分成
条直线最多可将平面分成![]() 个部分.现探究:空间内
个部分.现探究:空间内![]() 个平面最多可将空间分成多少个部分,
个平面最多可将空间分成多少个部分,![]() .设空间内
.设空间内![]() 个平面最多可将空间分成
个平面最多可将空间分成![]() 个部分.
个部分.
(1)求![]() 的值;
的值;
(2)用数学归纳法证明此结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 为椭圆的左、右焦点,点
为椭圆的左、右焦点,点![]() 在直线
在直线![]() 上且不在
上且不在![]() 轴上,直线
轴上,直线![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 和
和![]() ,
,![]() 为坐标原点.
为坐标原点.
![]() 设直线
设直线![]() 的斜率为
的斜率为![]() ,证明:
,证明:![]()
![]() 问直线
问直线![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 的斜率
的斜率![]() 满足
满足![]() ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果,其中的《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》,有丰富多彩的内容,是了解我国古代数学的重要文献,这5部专著中有3部产生于汉、魏、晋、南北朝时期,某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是汉、魏、晋、南北朝时期专著的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左右顶点,直线
的左右顶点,直线![]() 交
交![]() 于点
于点![]() ,
,![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点.当
为坐标原点.当![]() 为直角时,求直线
为直角时,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() ,圆C:
,圆C:![]() .
.
![]() 若过抛物线E的焦点F的直线l与圆C相切,求直线l方程;
若过抛物线E的焦点F的直线l与圆C相切,求直线l方程;
![]() 在
在![]() 的条件下,若直线l交抛物线E于A,B两点,x轴上是否存在点
的条件下,若直线l交抛物线E于A,B两点,x轴上是否存在点![]() 使
使![]() 为坐标原点
为坐标原点![]() ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com