
分析 (1)设切点为(m,0),则$\left\{\begin{array}{l}{3{m}^{2}+3a=0}\\{{m}^{3}+3am-2=0}\end{array}\right.$,即可求出a;
(2)分类讨论,求导数,确定函数的单调性,即可得出a的范围,使g(x)有极值,并求极大值与极小值的和;
(3)h(x)=x+2-$\frac{2}{{e}^{x}}$,在(-∞,+∞)上单调递增,其值域为R.则存在唯一x0∈R,使得h(x0)=a,分类讨论,利用函数f(x)在x=0处取得极小值,求a的取值范围.
解答 解:(1)设切点为(m,0),则$\left\{\begin{array}{l}{3{m}^{2}+3a=0}\\{{m}^{3}+3am-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{a=-1}\end{array}\right.$
∴a=-1时,x轴为曲线y=g(x)的切线. …(3分)
(2)g′(x)=3x2+3a
当a≥0时,g′(x)≥0成立,函数y=g(x)无极值
a<0,由g′(x)≥0,∴y=g(x)在(-∞,-$\sqrt{-a}$]和[$\sqrt{-a}$,+∞)上单增
由g′(x)≤0,∴y=g(x)在[-$\sqrt{-a}$,$\sqrt{-a}$]上单减
∴g(x)极大=g(-$\sqrt{-a}$),g(x)极小=g($\sqrt{-a}$),g(x)极大+g(x)极小=g(-$\sqrt{-a}$)+g($\sqrt{-a}$)=-4,
∴a<0时,函数y=g(x)有极值,g(x)极大+g(x)极小=-4 …(7分)
(3)f(x)=(x2-ax+a)ex-x2,
f′(x)=x[(x+2-a)ex-2],x∈R,
令f′(x)=0,则x=0或x+2-$\frac{2}{{e}^{x}}$-a=0,即x=0或h(x)=a,
∵h(x)=x+2-$\frac{2}{{e}^{x}}$,在(-∞,+∞)上单调递增,其值域为R.
∴存在唯一x0∈R,使得h(x0)=a,
①若x0>0,当x∈(-∞,0)时,h(x)<a,f′(x)>0;当x∈(0,x0)时,h(x)<a,f′(x)<0;∴f(x)在x=0处取得极大值,这与题设矛盾;
②若x0=0,当x∈(-∞,0)时,h(x)<a,f′(x)>0;当x∈(0,+∞)时,h(x)>a,f(x)>0;∴f(x)在x=0处不取极值,这与题设矛盾;
③若x0<0,当x∈(x0,0)时,h(x)>a,f′(x)<0;当x∈(0,+∞)时,h(x)>a,f′(x)>0;∴f(x)在x=0处取得极小值;
综上所述,x0<0,∴a=h(x0)<h(0)=0.
∴a的取值范围是(-∞,0). …(12分)
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的极值,考查分类讨论的数学思想,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{n(2{n}^{2}-n-1)}{2}$ | B. | n(n2-1) | C. | n3-1 | D. | $\frac{n({n}^{2}-1)}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 极小值-$\frac{1}{4}$,极大值0 | B. | 极小值0,极大值-$\frac{1}{4}$ | ||
| C. | 极小值$\frac{1}{4}$,极大值0 | D. | 极小值0,极大值$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2n-1)2-1=4n2-4n | B. | (3n-1)2-1=9n2-6n | C. | (2n+1)2-1=4n2+4n | D. | (3n+1)2-1=9n2+6n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
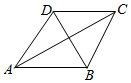 如图所示,四边形ABCD中,AB=AD=2,△BCD为正三角形,设∠BAD=α(α∈(0,π)).
如图所示,四边形ABCD中,AB=AD=2,△BCD为正三角形,设∠BAD=α(α∈(0,π)).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2\sqrt{2},+∞)$ | B. | $(4-2\sqrt{2},+∞)$ | C. | (4,+∞) | D. | $(4+2\sqrt{2},+∞)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com