Question

【题目】函数f（x）=xln（ax+1）（a≠0）．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）若a＞0且满足：对x1 ， x2∈[﹣1，1]，都有|f（x1）﹣f（x2）|≤ln3﹣ln2，试比较ea﹣1与 的大小，并证明．

Answer 1

【答案】解：（Ⅰ） ， ． 当a＞0时，f'（x）＞0，f'（x）单调递增，又f'（0）=0，
所以当 时，f'（x）＜0，f（x）单调递减；
当x∈（0，+∞）时，f'（x）＞0，f（x）单调递增；
当a＜0时，f'（x）＜0，f'（x）单调递减，又f'（0）=0，
所以当x∈（﹣∞，0）时，f'（x）＞0，f（x）单调递增；
当 时，f'（x）＜0，f（x）单调递减．
（Ⅱ）当a＞0时，由 得a≤1．
由（Ⅰ）知f（x）在[﹣1，0]上单调递减，在[0，1]上单调递增，
所以对x1 ， x2∈[﹣1，1]，都有|f（x1）﹣f（x2）|≤ln3﹣ln2，
等价于 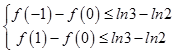即 解得 ；
令 ，g′（x）=1﹣（1﹣ ） ，
时，g'（x）＜0，g（x）单调递减；
当 时，g'（x）＞0，g（x）单调递增；
又 ，所以 ．
即 ，所以
【解析】（Ⅰ）求出函数的导数，通过讨论a的范围，求出函数的单调区间即可；（Ⅱ）问题等价于 ，解得a的范围，令 ，根据函数的单调性证明即可．
【考点精析】通过灵活运用利用导数研究函数的单调性，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减即可以解答此题．