
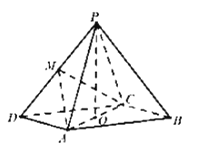
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() 为
为![]() 中点,
中点, ![]() 的中点.
的中点.
证明: ![]() ;
;
求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
![]()
| 应该取消 | 应该保留 | 无所谓 | |
在校学生 | 2100人 | 120人 | y人 | |
社会人士 | 600人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(1)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知以
中,已知以![]() 为圆心的圆的方程为:
为圆心的圆的方程为: ![]() ,以
,以![]() 为圆心的圆的方程为:
为圆心的圆的方程为: ![]() .
.
(1)若过点![]() 的直线
的直线![]() 沿
沿![]() 轴向左平移3个单位,沿
轴向左平移3个单位,沿![]() 轴向下平移4个单位后,回到原来的位置,求直线
轴向下平移4个单位后,回到原来的位置,求直线![]() 被圆
被圆![]() 截得的弦长;
截得的弦长;
(2)圆![]() 是以1为半径,圆心在圆
是以1为半径,圆心在圆![]() :
: ![]() 上移动的动圆 ,若圆
上移动的动圆 ,若圆![]() 上任意一点
上任意一点![]() 分别作圆
分别作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求
,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点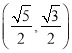 ,离心率为
,离心率为![]() ,点
,点![]() 坐标原点.
坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的左焦点
的左焦点![]() 任作一条不垂直于坐标轴的直线
任作一条不垂直于坐标轴的直线![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点,记弦
两点,记弦![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]() 的垂线
的垂线![]() 交直线
交直线![]() 于点
于点![]() ,证明:点
,证明:点![]() 在一条定直线上.
在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△OAB的顶点坐标为O(0,0),A(2,9),B(6,﹣3),点P的横坐标为14,且 ![]() ,点Q是边AB上一点,且
,点Q是边AB上一点,且 ![]() .
.
(1)求实数λ的值与点P的坐标;
(2)求点Q的坐标;
(3)若R为线段OQ上的一个动点,试求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
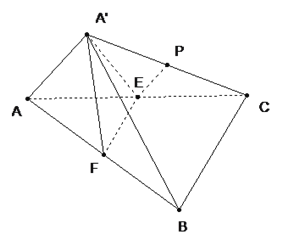
【题目】如图, ![]() 、
、![]() 分别为直角三角形
分别为直角三角形![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起到
折起到![]() 的位置,连结
的位置,连结![]() 、
、![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;(2)求证:平面
;(2)求证:平面![]() 平面
平面![]() ;
;
(3)求证: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=1,an+1=2an+1,b1=4,bn﹣bn﹣1=an+1(n≥2).
(1)求证:数列{an+1}是等比数列;
(2)求数列{an},{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(1,2)
=(1,2)
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求v与
垂直,求v与 ![]() 的夹角θ.
的夹角θ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com