
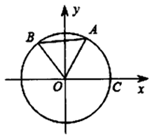
 如图,在平面直角坐标系xoy中,A,B,C均为⊙O上的点,其中A($\frac{3}{5}$,$\frac{4}{5}$),C(1,0),点B在第二象限.
如图,在平面直角坐标系xoy中,A,B,C均为⊙O上的点,其中A($\frac{3}{5}$,$\frac{4}{5}$),C(1,0),点B在第二象限.分析 (1)由题意,cosθ=$\frac{3}{5}$,sinθ=$\frac{4}{5}$,tanθ=$\frac{4}{3}$,再利用二倍角公式,即可求tan2θ的值;
(2)利用三角函数的定义,即可求点B的坐标.
解答 解:(1)由题意,cosθ=$\frac{3}{5}$,sinθ=$\frac{4}{5}$,tanθ=$\frac{4}{3}$,
∴tan2θ=$\frac{2×\frac{4}{3}}{1-\frac{16}{9}}$=-$\frac{24}{7}$;
(2)∵△AOB为正三角形,
∴cos(θ+60°)=$\frac{3-4\sqrt{3}}{10}$,sin(θ+60°)=$\frac{4+3\sqrt{3}}{10}$,
∴B($\frac{3-4\sqrt{3}}{10}$,$\frac{4+3\sqrt{3}}{10}$).
点评 本题考查任意角的三角函数的定义,考查二倍角的正弦,属于基础题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤1} | B. | {x|1≤x≤3} | C. | {x|0<x≤1} | D. | {x|0<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10,15,25 | B. | 10,16,24 | C. | 11,15,24 | D. | 12,13,25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com