
【题目】已知函数![]() ,要使函数
,要使函数![]() 恰有一个零点,则实数
恰有一个零点,则实数![]() 的取值范围是( ).
的取值范围是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】B
【解析】
先利用导数求出函数![]() 的单调性和极值,画出函数
的单调性和极值,画出函数![]() 的大致图象,令
的大致图象,令![]() ,由函数
,由函数![]() 的图象可知方程
的图象可知方程![]() ,只能有一个正根,且若有负根的话,负根必须小于
,只能有一个正根,且若有负根的话,负根必须小于![]() ,分类讨论,即可求解.
,分类讨论,即可求解.
由题意,函数![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
所以函数![]() 的最小值为
的最小值为![]() ,
,
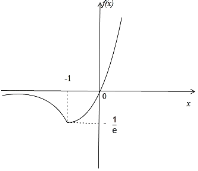
函数![]() 的大致图象,如图所示:
的大致图象,如图所示:
函数![]() 恰有一个零点,
恰有一个零点,
等价于方程![]() 只有一个根,
只有一个根,
令![]() ,由函数
,由函数![]() 的图象可知方程
的图象可知方程![]() ,只能有一个正根,且若有负根的话,负根必须小于
,只能有一个正根,且若有负根的话,负根必须小于![]() ,
,
①当![]() 时,方程为
时,方程为![]() ,∴
,∴![]() ,符合题意,
,符合题意,
②当![]() 时,
时,
若![]() ,即
,即![]() 时,方程为
时,方程为![]() ,解得
,解得![]() ,符合题意,
,符合题意,
若![]() ,即
,即![]() 时:设
时:设![]() ,
,
(ⅰ)当![]() 时,二次函数
时,二次函数![]() 开口向下,又
开口向下,又![]() ,
,
要使方程![]() 只有一个正根,且负根小于
只有一个正根,且负根小于![]() ,则
,则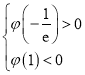 ,
,
即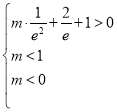 ,可得
,可得![]() ,
,
(ⅱ)当![]() 时,二次函数
时,二次函数![]() 开口向上,又因为
开口向上,又因为![]() ,
,
则方程![]() 有两个不等的正根,不符合题意,
有两个不等的正根,不符合题意,
综上所求,实数![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ,
,
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设a是实数,关于z的方程(z2-2z+5)(z2+2az+1)=0有4个互不相等的根,它们在复平面上对应的4个点共圆,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,若问题中的正整数k存在,求k的值;若k不存在,请说明理由.
这三个条件中任选一个,补充在下面问题中,若问题中的正整数k存在,求k的值;若k不存在,请说明理由.
设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() 是等比数列,______,
是等比数列,______,![]() ,
,![]() ,
,![]() .是否存在k,使得
.是否存在k,使得![]() 且
且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,圆心为坐标原点的单位圆O在C的内部,且与C有且仅有两个公共点,直线
,圆心为坐标原点的单位圆O在C的内部,且与C有且仅有两个公共点,直线![]() 与C只有一个公共点.
与C只有一个公共点.
(1)求C的标准方程;
(2)设不垂直于坐标轴的动直线l过椭圆C的左焦点F,直线l与C交于A,B两点,且弦AB的中垂线交x轴于点P,试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区![]() 的
的![]() 天日落和夜晚天气,得到如下
天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气日落云里走 | 下雨 | 未下雨 |
出现 |
|
|
未出现 |
|
|
参考公式: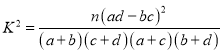 .
.
临界值表:
|
|
|
|
|
|
|
|
|
|
(1)根据上面的列联表判断能否有![]() 的把握认为“当晚下雨”与“‘日落云里走’出现”有关?
的把握认为“当晚下雨”与“‘日落云里走’出现”有关?
(2)小波同学为进一步认识其规律,对相关数据进行分析,现从上述调查的“夜晚未下雨”天气中按分层抽样法抽取![]() 天,再从这
天,再从这![]() 天中随机抽出
天中随机抽出![]() 天进行数据分析,求抽到的这
天进行数据分析,求抽到的这![]() 天中仅有
天中仅有![]() 天出现“日落云里走”的概率.
天出现“日落云里走”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() .
.
(Ⅰ)求曲线![]() 被直线
被直线![]() 截得的弦长;
截得的弦长;
(Ⅱ)与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,求点
,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是我国古代计算圆周率![]() 的一种方法.在公元
的一种方法.在公元![]() 年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求
年左右,由魏晋时期的数学家刘徽发明.其原理就是利用圆内接正多边形的面积逐步逼近圆的面积,进而求![]() .当时刘微就是利用这种方法,把
.当时刘微就是利用这种方法,把![]() 的近似值计算到
的近似值计算到![]() 和
和![]() 之间,这是当时世界上对圆周率
之间,这是当时世界上对圆周率![]() 的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率
的计算最精确的数据.这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的,用有限的来逼近无穷的.为此,刘微把它概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这种方法极其重要,对后世产生了巨大影响,在欧洲,这种方法后来就演变为现在的微积分.根据“割圆术”,若用正二十四边形来估算圆周率![]() ,则
,则![]() 的近似值是( )(精确到
的近似值是( )(精确到![]() )(参考数据
)(参考数据![]() )
)

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的左右焦点分别为F1,F2,点
的左右焦点分别为F1,F2,点![]() 在椭圆C上,满足
在椭圆C上,满足![]() .
.
(1)求椭圆C的标准方程;
(2)直线l1过点P,且与椭圆只有一个公共点,直线l2与l1的倾斜角互补,且与椭圆交于异于点P的两点M,N,与直线x=1交于点K(K介于M,N两点之间).
①问:直线PM与PN的斜率之和能否为定值,若能,求出定值并写出详细计算过程;若不能,请说明理由;
②求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,AB∥CD,
中,AB∥CD,![]() ,且
,且![]() .现以
.现以![]() 为一边向梯形外作正方形
为一边向梯形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,如图2.
垂直,如图2.


(Ⅰ)求证:BC⊥平面DBE;
(Ⅱ)求点D到平面BEC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com