求过点M(4.4).并与椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1相切的直线方程．题目和参考答案——青夏教育精英家教网—

15．求过点M（4，4），并与椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1相切的直线方程．

分析讨论直线的斜率不存在和存在，设过点M（4，4）的直线方程为y-4=k（x-4），代入椭圆方程，可得含k的二次方程，由判别式为0，解得k，进而得到所求直线方程．

解答解：当直线的斜率不存在时，直线x=4与椭圆相切；
当直线的斜率存在时，设过点M（4，4）的直线方程为y-4=k（x-4），
即有y=kx+4-4k，代入椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1，
可得（9+16k²）x²+128k（1-k）x+16（4-4k）²-144=0，
由直线和椭圆相切的条件可得
△=（128k（1-k））²-4（9+16k²）（16（4-4k）²-144）=0，
化简可得32k-7=0，
解得k=$\frac{7}{32}$，
即有所求直线方程为y=$\frac{7}{32}$x+$\frac{25}{8}$
或x=4．

点评本题考查椭圆的方程的运用，考查直线和椭圆相切的条件，考查运算能力，属于中档题．

练习册系列答案

寒假作业时代出版传媒股份有限公司系列答案

寒假作业华中科技大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

5．

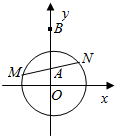己知圆O：x²十y²=l，及A（0，$\sqrt{2}$-l），B（0，$\sqrt{2}$+l）：
①P是x轴上动点，当∠APB最大时，p点坐标为（±$\sqrt{2}$，0）
②过A任作一条直线，与圆O交于M、N，则$\frac{|NA|}{|NB|}$=$\sqrt{2}$-1．
③过A任作一条直线，与圆O交于M、N，则$\frac{|NA|}{|NB|}$=$\frac{|MA|}{|MB|}$成立
④任作一条直线与圆O交于M、N，则仍有$\frac{|NA|}{|NB|}$=$\frac{|MA|}{|MB|}$．
上述说法正确的是②③④．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．已知函数$f（x）=\sqrt{x+3}+\sqrt{4-x}$的定义域为集合A，g（x）=lg（5-x）+lg（x+1）的定义域为集合B．设全集U=R，求A∩B及（∁_UA）∩B．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

3．若$y={log_{3{a^2}-1}}x$在（0，+∞）内为增函数，且y=a^-x也为增函数，则a的取值范围是（　　）

A．

$（\frac{{\sqrt{3}}}{3}，\;\;1）$

B．

$（0，\;\;\frac{1}{3}）$

C．

$（\frac{{\sqrt{3}}}{3}，\;\;\frac{{\sqrt{6}}}{3}）$