
(本小题14分)
如图,在四棱锥V-ABCD中底面ABCD是正方形,侧面VAD是正三角形,平面VAD
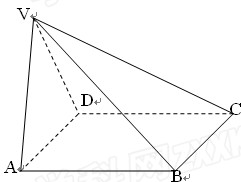
(1)证 明:AB
明:AB ;
;
(2)求面VAD与面VDB所成的二面角的余弦值。
本题14分)
方法一:(用传统方法)(1)证明:平面VAD 平面ABCD,AB
平面ABCD,AB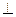 AD,AB
AD,AB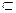 平面ABCD,
平面ABCD,
面VAD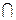 ABCD=AD,
ABCD=AD,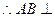 面VAD
面VAD
(2) 取VD中点E,连接AE,BE,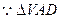 是正三角形,
是正三角形,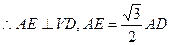
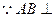 面VAD, AE,
面VAD, AE,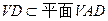
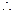 AB
AB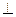 VD,AB
VD,AB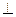 AE
AE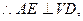 AB
AB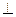 VD, AB
VD, AB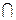 AE=A,且AB,AE
AE=A,且AB,AE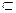 平面ABE,
平面ABE, 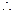 VD
VD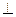 平面ABE,
平面ABE, 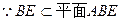 ,
,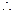 BE
BE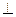 VD,
VD,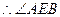 是所求的二面角的平面角。
是所求的二面角的平面角。
在RT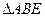 中,
中,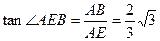 ,
,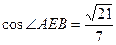
方法二:(空间向量法)以D为坐标原点,建立空间直角坐标系如图
(1)证明:不妨设A(1,0,0), B(1,1,0), 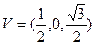 ,
,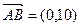 ,
,
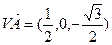 ,
,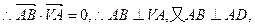 因此AB与平面VAD内两条相交直线VA,AD都垂直,
因此AB与平面VAD内两条相交直线VA,AD都垂直, 面VAD
面VAD
(2)取VD的中点E,则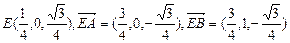 ,
,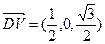 ,由
,由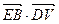 =0,得
=0,得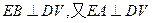 ,因此
,因此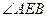 是所求二面角的平面角。
是所求二面角的平面角。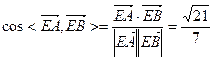
解析


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:2011-2012学年广东省肇庆市高三复习必修五综合练习 题型:解答题
(本小题14分)如图所示,L是海面上一条南北方向的海防警戒线,在L上点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20 km处和54 km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20 s后监测点C相继收到这一信号.在当时气象条件下,声波在水中的传播速度是1. 5 km/s.
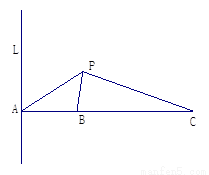
(1)设A到P的距离为 km,用
km,用 分别表示B、C到P 的距离,并求
分别表示B、C到P 的距离,并求 值;
值;
(2)求静止目标P到海防警戒线L的距离(结果精确到0.01 km)
查看答案和解析>>
科目:高中数学 来源:2011年江苏省高一上学期期末考试数学试卷 题型:解答题
(本小题14分)
如图,已知 的面积为14,
的面积为14, 、
、 分别为边
分别为边 、
、 上的点,且
上的点,且


 ,
, 与
与 交于
交于 。设存在
。设存在 和
和 使
使 ,
, ,
, ,
, 。
。
(1)求 及
及
(2)用 ,
, 表示
表示
(3)求 的面积
的面积
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二上学期期末考试理科数学试卷 题型:解答题
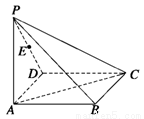
(本小题14分)如图所示,在四棱锥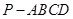 中,底面
中,底面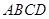 为矩形,侧棱
为矩形,侧棱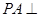 底面
底面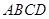 ,
, 为
为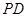 的中点.
的中点.
(1)求直线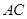 与
与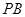 所成角的余弦值;
所成角的余弦值;
(2)在侧面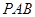 内找一点
内找一点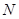 ,使
,使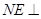 平面
平面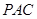 ,并分别求出点
,并分别求出点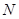 到
到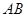 和
和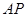 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源:宁波市2010届高三三模考试文科数学试题 题型:解答题
(本小题14分)如图,三棱锥 中,
中, 平面
平面 ,
,
 ,
, ,
, 分别是
分别是 上
上
的动点,且 平面
平面 ,二面角
,二面角 为
为 .
.
(1)求证: 平面
平面 ;
;
(2)若 ,求直线
,求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省扬州市高三第四次模拟考试数学试题 题型:解答题
(本小题14分)
如图,在直三棱柱 中,
中, ,点
,点 在边
在边 上,
上, 。
。
(1)求证: 平面
平面 ;
;
(2)如果点 是
是 的中点,求证:
的中点,求证: 平面
平面 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com