
【题目】函数![]() 的定义域为
的定义域为![]() ,且对任意
,且对任意![]() ,有
,有![]() ,且当
,且当![]() 时
时![]() .
.
(1)证明:![]() 是奇函数;
是奇函数;
(2)证明:![]() 在
在![]() 上是减函数;
上是减函数;
(3)求![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)证明见解析;(2)证明见解析;(3) 最大值是6,最小值是-6.
【解析】
(1)令x=y=0,则可得f(0)=0;y=﹣x,即可证明f(x)是奇函数,
(2)设x1>x2,由已知可得f(x1﹣x2)<0,再利用f(x+y)=f(x)+f(y),及减函数的定义即可证明.
(3)由(2)的结论可知f(﹣3)、f(3)分别是函数y=f(x)在[﹣3、3]上的最大值与最小值,故求出f(﹣3)与f(3)就可得所求值域.
(1)因为![]() 的定义域为
的定义域为![]() ,且
,且![]() ,
,
令![]() 得
得![]() ,所以
,所以![]() ;
;
令![]() ,则
,则![]() ,所以
,所以![]() ,
,
从而有![]() ,所以
,所以![]() ,所以
,所以![]() 是奇函数.
是奇函数.
(2)任取![]() ,且
,且![]() ,
,
则![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,从而
,从而![]() 在
在![]() 上是减函数.
上是减函数.
(3)由于![]() 在
在![]() 上是减函数,
上是减函数,
故![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]() ,
,
由于![]() ,所以
,所以![]()
![]() ,
,
由于![]() 为奇函数知,
为奇函数知, ![]() ,
,
从而![]() 在区间
在区间![]() 上的最大值是6,最小值是
上的最大值是6,最小值是![]() 6.
6.


科目:高中数学 来源: 题型:
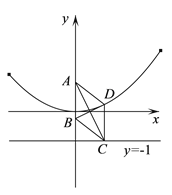
【题目】已知菱形![]() ,
,![]() 在
在![]() 轴上且
轴上且![]() ,
,![]()
![]() (
(![]() ,
,![]() ).
).
(Ⅰ)求![]() 点轨迹
点轨迹![]() 的方程;
的方程;
(Ⅱ)延长![]() 交轨迹
交轨迹![]() 于点
于点![]() ,轨迹
,轨迹![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 交于点
交于点![]() ,试判断以
,试判断以![]() 为圆心,线段
为圆心,线段![]() 为半径的圆与直线
为半径的圆与直线![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保护农民种粮收益,促进粮食生产,确保国家粮食安全,调动广大农民粮食生产的积极性,从2004年开始,国家实施了对种粮农民直接补贴.通过对2014~2018年的数据进行调查,发现某地区发放粮食补贴额![]() (亿元)与该地区粮食产量
(亿元)与该地区粮食产量![]() (万亿吨)之间存在着线性相关关系.统计数据如下表:
(万亿吨)之间存在着线性相关关系.统计数据如下表:
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
补贴额 | 9 | 10 | 12 | 11 | 8 |
粮食产量 | 23 | 25 | 30 | 26 | 21 |
(1)请根据如表所给的数据,求出![]() 关于
关于![]() 的线性回归直线方程
的线性回归直线方程![]() ;
;
(2)通过对该地区粮食产量的分析研究,计划2019年在该地区发放粮食补贴额7亿元,请根据(1)中所得的线性回归直线方程,预测2019年该地区的粮食产量.
(参考公式: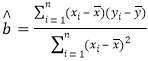 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中![]() 中,直线
中,直线![]() ,圆
,圆![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求直线![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下:1.12,1.25,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42.据此可估计该生产线上大约有25%的零件内径小于等于___________㎜,大约有30%的零件内径大于___________mm(单位:mm).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com