
【题目】. (12分)如图所示,函数![]() 的一段图象过点
的一段图象过点![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得函数
个单位,得函数![]() 的图象,求函数
的图象,求函数![]() 的最大值,并求此时自变量
的最大值,并求此时自变量![]() 的取值集合.
的取值集合.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由图知,T=π,从而知ω=2,由2×(![]() )+φ=0,可求得φ,f1(0)=1可求得A,从而可求函数f1(x)的表达式;
)+φ=0,可求得φ,f1(0)=1可求得A,从而可求函数f1(x)的表达式;
(2)利用函数y=Asin(ωx+φ)的图象变换,可求得y=f2(x)=f1(x![]() )=2sin(2x
)=2sin(2x![]() ),从而可求y=f2(x)的最大值及取最大值时的自变量的值.
),从而可求y=f2(x)的最大值及取最大值时的自变量的值.
(1)由图知,T![]() (
(![]() )=π,
)=π,
∴ω![]() 2;
2;
又2×(![]() )+φ=0,
)+φ=0,
∴φ![]() ,
,
∴f1(x)=Asin(2x![]() ),
),
又f1(0)=1,即Asin![]() 1,
1,
∴A![]() 2,
2,
∴f1(x)=2sin(2x![]() );
);
(2)∵y=f2(x)=f1(x![]() )=2sin[2(x
)=2sin[2(x![]() )
)![]() ]=2sin(2x
]=2sin(2x![]() ),
),
∴当2x![]() 2kπ
2kπ![]() (k∈Z),即{x|x=kπ
(k∈Z),即{x|x=kπ![]() (k∈Z)}时,y=f2(x)取得最大值2.
(k∈Z)}时,y=f2(x)取得最大值2.
又-![]() 2x
2x![]() ,解得-
,解得-![]() x
x![]() +
+![]() ,(k∈Z),
,(k∈Z),
所以![]() 的增区间为
的增区间为![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax﹣1|
(1)若f(x)≤2的解集为[﹣3,1],求实数a的值;
(2)若a=1,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤3﹣2m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)= ![]() .
.
(1)证明方程f(x)=g(x)在区间(1,2)内有且仅有唯一实根;
(2)记max{a,b}表示a,b两个数中的较大者,方程f(x)=g(x)在区间(1,2)内的实数根为x0 , m(x)=max{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)内有两个不等的实根x1 , x2(x1<x2),判断x1+x2与2x0的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|.
(1)当a=2时,解不等式f(x)≥7﹣|x﹣1|;
(2)若f(x)≤1的解集为[0,2], ![]() =a(m>0,n>0),求证:m+4n≥2
=a(m>0,n>0),求证:m+4n≥2 ![]() +3.
+3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() .
.
(![]() )求
)求![]() 的顶点
的顶点![]() 、
、![]() 的坐标.
的坐标.
(![]() )若圆
)若圆![]() 经过不同的三点
经过不同的三点![]() 、
、![]() 、
、![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求证:函数f(x)-g(x)必有零点;
(2)设函数G(x)=f(x)-g(x)-1
①若函数G(x)有两相异零点且![]() 在
在![]() 上是减函数,求实数m的取值范围。
上是减函数,求实数m的取值范围。
②是否存在整数a,b使得![]() 的解集恰好为
的解集恰好为![]() 若存在,求出a,b的值,若不存在,请说明理由。
若存在,求出a,b的值,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDE中,四边形ABED是直角梯形,∠BAD=90°,DE∥AB,△ACD是的正三角形,CD=AB=![]() DE=1,BC=
DE=1,BC=![]()
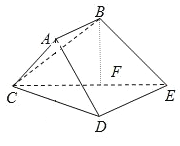
(1)求证:△CDE是直角三角形
(2) F是CE的中点,证明:BF⊥平面CDE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com