
如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是 ( ).

A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-7-2练习卷(解析版) 题型:填空题
设非零常数d是等差数列x1,x2,x3,…,x19的公差,随机变量ξ等可能地取值x1,x2,x3,…,x19,则方差D(ξ)=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-6-1练习卷(解析版) 题型:解答题
已知直线l:y=x+m,m∈R.
(1)若以点M(2,0)为圆心的圆与直线l相切于点P,且点P在y轴上,求该圆的方程;
(2)若直线l关于x轴对称的直线为l′,问直线l′与抛物线C:x2=4y是否相切?说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-3练习卷(解析版) 题型:选择题
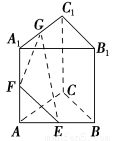
正三棱柱ABC-A1B1C1的棱长都为2,E,F,G为AB,AA1,A1C1的中点,则B1F与平面GEF所成角的正弦值为( ).
A.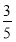 B.
B.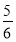 C.
C.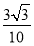 D.
D.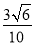
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-2练习卷(解析版) 题型:解答题
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.

(1)求证:BC⊥平面PAC;
(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-1练习卷(解析版) 题型:解答题
有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-5-1练习卷(解析版) 题型:选择题
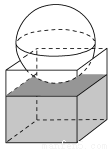
如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( ).
A.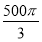 cm3 B.
cm3 B.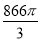 cm3 C.
cm3 C. 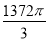 cm3 D.
cm3 D.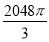 cm3
cm3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-4-1练习卷(解析版) 题型:填空题
将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
11 12 13 14 15
……
根据以上排列规律,数阵中第n(n≥3)行从左至右的第3个数是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮专题复习知能提升演练1-2-2练习卷(解析版) 题型:解答题
设函数f(x)=x3-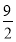 x2+6x-a.
x2+6x-a.
(1)对于任意实数x,f′(x)≥m恒成立,求m的最大值;
(2)若方程f(x)=0有且仅有一个实根,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com