Question

已知函数的图象经过四个象限，则实数的取值范围是      

Answer 1

解析试题分析：求函数的极值，要使图象经过四个象限只要两极值符号不同即可．解：求导函数可得f′（x）=ax²+ax-b，∵函数∴f′（x）=ax²+ax-2a=a（x+2）（x-1），令f′（x）=a（x+2）（x-1）=0得x=-2或x=1，x∈（-∞，-2）时f′（x）的符号与x∈（-2，1）时f′（x）的符号相反，x∈（-2，1）时f′（x）的符号与x∈（1，+∞）时f′（x）的符号相反，∴函数在-2与1处取极值
∵图象经过四个象限，∴f（-2）•f（1）＜0，即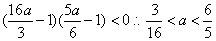 
考点：导数知识的运用
点评：本题考查导数知识的运用，考查导数的几何意义，考查函数的极值，利用两极值符号不同是关键