
先阅读下列不等式的证法,再解决后面的问题:
已知a1,a2∈R,a1+a2=1,求证: +
+ ≥
≥ .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,f(x)对一切实数x∈R,恒有f(x)≥0,则Δ=4-8( +
+ )≤0,∴
)≤0,∴ +
+ ≥
≥ .
.
(1)已知a1,a2,…,an∈R,a1+a2+…+an=1,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
科目:高中数学 来源: 题型:解答题
设函数f(x)=x-xlnx,数列{an}满足0<a1<1,an+1=f(an).求证:
(1)函数f(x)在区间(0,1)是增函数;
(2)an<an+1<1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
数列 的前
的前 项组成集合
项组成集合 ,从集合
,从集合 中任取
中任取 个数,其所有可能的
个数,其所有可能的 个数的乘积的和为
个数的乘积的和为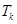 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记 .例如:当
.例如:当 时,
时, ,
, ,
,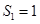 ;当
;当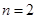 时,
时, ,
, ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)猜想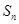 ,并用数学归纳法证明.
,并用数学归纳法证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com