
【题目】牛顿法求方程f(x)=0近似根原理如下:求函数y=f(x)在点(xn , f(xn))处的切线y=f′(xn)(x﹣xn)+f(xn),其与x轴交点横坐标xn+1=xn﹣ ![]() (n∈N*),则xn+1比xn更靠近f(x)=0的根,现已知f(x)=x2﹣3,求f(x)=0的一个根的程序框图如图所示,则输出的结果为( )
(n∈N*),则xn+1比xn更靠近f(x)=0的根,现已知f(x)=x2﹣3,求f(x)=0的一个根的程序框图如图所示,则输出的结果为( ) 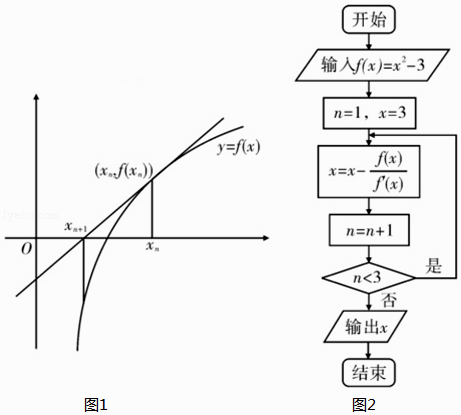
A.2
B.1.75
C.1.732
D.1.73
科目:高中数学 来源: 题型:
【题目】已知无穷数列{an}的各项都是正数,其前n项和为Sn , 且满足:a1=a,rSn=anan+1﹣1,其中a≠1,常数r∈N;
(1)求证:an+2﹣an是一个定值;
(2)若数列{an}是一个周期数列(存在正整数T,使得对任意n∈N* , 都有an+T=an成立,则称{an}为周期数列,T为它的一个周期,求该数列的最小周期;
(3)若数列{an}是各项均为有理数的等差数列,cn=23n﹣1(n∈N*),问:数列{cn}中的所有项是否都是数列{an}中的项?若是,请说明理由,若不是,请举出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处发现北偏东
处发现北偏东![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处有一艘走私船.在
处有一艘走私船.在![]() 处北偏西
处北偏西![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处的我方缉私船奉命以
处的我方缉私船奉命以![]() 海里
海里![]() 小时的速度追截走私船,此时走私船正以
小时的速度追截走私船,此时走私船正以![]() 海里
海里![]() 小时的速度从
小时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:缉私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623——1662)是在1654年发现这一规律的,比杨辉要迟![]() 年,比贾宪迟
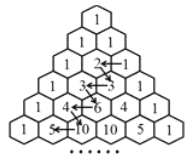
年,比贾宪迟![]() 年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了,这又是我国数学史上的一个伟大成就。如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:
年。如图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了,这又是我国数学史上的一个伟大成就。如图所示,在“杨辉三角”中,从1开始箭头所指的数组成一个锯齿形数列:![]() ,则此数列前
,则此数列前![]() 项和为________.
项和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c﹣a)cosB﹣bcosA=0.
(Ⅰ)求角B的大小;
(Ⅱ)求 ![]() sinA+sin(C﹣
sinA+sin(C﹣ ![]() )的取值范围.
)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子产品公司前四年的年宣传费x(单位:千万元)与年销售量y(单位:百万部)的数据如下表所示:
x(单位:千万元) | 1 | 2 | 3 | 4 |
y(单位:百万部) | 3 | 5 | 6 | 9 |
可以求y关于x的线性回归方程为 ![]() =1.9x+1.
=1.9x+1.
参考公式:回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .
.
x(单位:千万元) | 1 | 2 | 3 | 4 | 10 |
y(单位:百万部) | 3 | 5 | 6 | 9 | m |
并利用小二乘法的原理说明 ![]() =
= ![]() x+
x+ ![]() 与
与 ![]() =1.9x+1的关系.
=1.9x+1的关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知曲线C1的参数方程为 ![]() ,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
(Ⅰ)求C1的极坐标方程与C2的直角坐标方程;
(Ⅱ)若P是C1上任意一点,过点P的直线l交C2于点M,N,求|PM||PN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
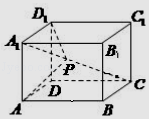
【题目】如图,在长方体ABCD﹣A1B1C1D1中, ![]() ,点P为线段A1C上的动点(包含线段端点),则下列结论正确的 . ①当
,点P为线段A1C上的动点(包含线段端点),则下列结论正确的 . ①当 ![]() 时,D1P∥平面BDC1;
时,D1P∥平面BDC1;
②当 ![]() 时,A1C⊥平面D1AP;
时,A1C⊥平面D1AP;
③当∠APD1的最大值为90°;
④AP+PD1的最小值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+be﹣x﹣2asinx(a,b∈R).
(1)当a=0时,讨论函数f(x)的单调区间;
(2)当b=﹣1时,若f(x)>0对任意x∈(0,π)恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com