
【题目】2020年新型冠状病毒肺炎(简称“新冠肺炎”)成为威胁全球的公共卫生问题,中医药在本次新冠肺炎的治疗中发挥了重要作用.研究人员对66例普通型新冠肺炎恢复期患者进行了中医临床特征分析,发现主要证型有气阴两虚证与肺脾气虚证,同时可能兼夹湿证.为研究这两种主要证型在兼夹湿证的难易上是否有差异,研究人员将湿证症状分级量化,将所有肺脾气虚证患者的量化分作成茎叶图.
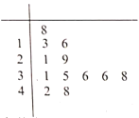
(1)若量化分不低于16分,即可诊断为兼夹湿证,请参考茎叶图,完成下面![]() 列联表.
列联表.
夹湿证 | 非夹湿证 | 合计 | |
气阴两虚 | 20 | ||
肺脾气虚 | |||
合计 | 66 |
(2)根据此资料,能否有99%的把握认为两种主要证型在兼夹湿证的难易上有差异?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
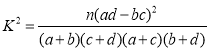
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,点A,B的坐标分别为![]() ,
,![]() ,P是坐标平面内的动点,且直线
,P是坐标平面内的动点,且直线![]() ,
,![]() 的斜率之积等于
的斜率之积等于![]() .设点P的轨迹为C.
.设点P的轨迹为C.
(1)求轨迹C的方程;
(2)某同学对轨迹C的性质进行探究后发现:若过点![]() 且倾斜角不为0的直线
且倾斜角不为0的直线![]() 与轨迹C相交于M,N两点,则直线
与轨迹C相交于M,N两点,则直线![]() ,
,![]() 的交点Q在一条定直线上.此结论是否正确?若正确,请给予证明,并求出定直线方程;若不正确,请说明理由.
的交点Q在一条定直线上.此结论是否正确?若正确,请给予证明,并求出定直线方程;若不正确,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式
满足关系式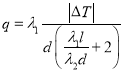 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米·度),不流通、干燥空气的热传导系数
焦耳/(厘米·度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 为室内外温度差,
为室内外温度差,![]() 值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 | 玻璃间夹空气层厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
则保温效果最好的双层玻璃的型号是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() .
.
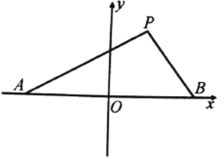
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为
的轨迹为![]() ,点
,点![]() 是轨迹为
是轨迹为![]() 上不同于
上不同于![]() 的两点,且满足
的两点,且满足![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
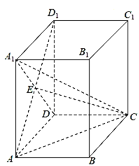
(1)证明:AE⊥平面ECD;
(2)求点C1到平面AEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 中,棱
中,棱![]() ,
,![]() 所在直线所成角为
所在直线所成角为![]() ,且
,且![]() ,
,![]() ,
,![]() ,面
,面![]() 和面
和面![]() 所成的锐二面角为
所成的锐二面角为![]() ,面
,面![]() 和面
和面![]() 所成的锐二面角为
所成的锐二面角为![]() ,当四面体
,当四面体![]() 的体积取得最大值时( ).
的体积取得最大值时( ).
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年4月8日,武汉市雷神山医院为确诊新型冠状病毒肺炎患者,需要检测核酸是否为阳性,现有![]() 份核酸样本,有以下两种检测方式:(1)逐份检测,则需要检测
份核酸样本,有以下两种检测方式:(1)逐份检测,则需要检测![]() 次;(2)混合检测,将其中
次;(2)混合检测,将其中![]() (
(![]() ,且
,且![]() )份核酸样本分别取样混合在一起检测,若检测结果为阴性,这
)份核酸样本分别取样混合在一起检测,若检测结果为阴性,这![]() 份核酸样本全为阴性,因而这
份核酸样本全为阴性,因而这![]() 份核酸样本只要检测一次就够了,如果检测结果为阳性,为了明确这
份核酸样本只要检测一次就够了,如果检测结果为阳性,为了明确这![]() 份核酸样本究竟哪几份为阳性,就要对这
份核酸样本究竟哪几份为阳性,就要对这![]() 份样本再逐份检测,此时这
份样本再逐份检测,此时这![]() 份核酸样本的检测次数总共为
份核酸样本的检测次数总共为![]() 次.假设在接受检测的核酸样本中,每份样本的检测结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检测的核酸样本中,每份样本的检测结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份核酸样本,其中只有2份样本为阳性,若采用逐份检测方式,求恰好经过4次检测就能把阳性样本全部检测出来的概率.
(2)现取其中![]() (
(![]() ,且
,且![]() )份核酸样本,记采用逐份检测方式,样本需要检测的总次数为
)份核酸样本,记采用逐份检测方式,样本需要检测的总次数为![]() ,采用混合检测方式,样本需要检测的总次数为
,采用混合检测方式,样本需要检测的总次数为![]() .
.
①试运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,用混合检测方式可以使得样本需要检测的总次数的期望值比逐份检测的总次数期望值更少,求
,用混合检测方式可以使得样本需要检测的总次数的期望值比逐份检测的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为
分别为![]() 内角
内角![]() 的对边,若
的对边,若![]() 是锐角三角形,需要同时满足下列四个条件中的三个:
是锐角三角形,需要同时满足下列四个条件中的三个:
①![]() ②
②![]() ③
③![]() ④
④![]()
(1)条件①④能否同时满足,请说明理由;
(2)以上四个条件,请在满足三角形有解的所有组合中任选一组,并求出对应的![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com