Question

如下图，已知两点P₁(4，9)和P₂(6，3)，

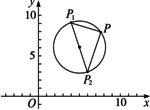
(1)求以P₁P₂为直径的圆的方程；

(2)试判断点M(6，9)、N(3，3)、Q(5，3)是在圆上、在圆内、还是在圆外？

(3)求以P₁为圆心，|P₁P₂|为半径的圆，并判断点M(6，9)、N(3，3)、Q(5，3)是在圆上、圆内、还是圆外？

Answer 1

答案：
解析：

　　(1)解法一：设圆心C(a，b)，半径r，则由C为P₁P₂的中点得a＝＝5，b＝＝6．

　　又由两点间的距离公式得r＝|CP₁|＝．

　　∴所求圆的方程为(x－5)²＋(y－6)²＝10．

　　解法二：∵半圆上的圆周角是直角，

　　∴对于圆上任一点P(x，y)，有PP₁⊥PP₂．·＝－1，即＝－1．

　　化简得x²＋y²－10x－12y＋51＝0，显然当点P与P₁、P₂重合时，也满足上述方程．综上，可知(x－5)²＋(y－6)²＝10为所求圆的方程．

　　(2)解：分别计算点到圆心的距离：|CM|＝；

　　|CN|＝；

　　|CQ|＝．

　　因此，点M在圆上，点N在圆外，点Q在圆内．

　　(3)解：由两点间的距离公式，得r＝|P₁P₂|＝．

　　所以以P₁为圆心，以|P₁P₂|为半径的圆的方程为(x－4)²＋(y－9)²＝40．

　　∵(6－4)²＋(9－9)²＝4＜40，(3－4)²＋(3－9)²＝37＜40，(5－4)²＋(3－9)²＝37＜40．

　　∴点M、N、Q都在圆内．

　　思路分析：对于本题中圆的方程可从两个角度来考虑：(1)从确定圆的条件考虑，需要求圆心和半径，可用待定系数法解决(解法一)．(2)从图形上动点P的性质考虑，用求曲线方程的一般方法解决(解法二)．

提示：

　　解法一从圆的两个要素入手，确定出圆心和半径，解法二则从动点的几何特征入手，将圆周角为直角这一特征用坐标加以表示．对于本题还可通过直角三角形斜边上的中线等于斜边的一半这一性质列方程求解．

　　另外，本题也可直接套用公式，即以点P₁(x₁，y₁)、P₂(x₂，y₂)为直径端点的圆的方程为(x－x₁)(x－x₂)＋(y－y₁)(y－y₂)＝0．