
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
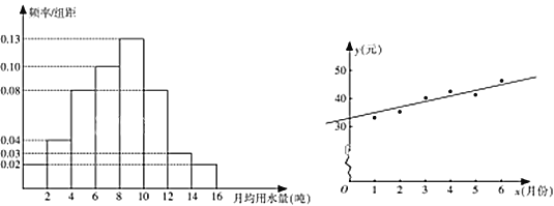
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
【答案】(Ⅰ)平均数为7.96,中位数为8.15;(Ⅱ)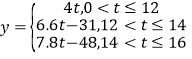 ;(Ⅲ)13吨.
;(Ⅲ)13吨.
【解析】试题分析:
本题考查频率分布直方图的应用及线性回归方程的应用。(Ⅰ)根据用频率分布直方图估计平均数、中位数的方法计算即可。(Ⅱ)结合题意可用分段函数表示出![]() 与
与![]() 的关系。(Ⅲ)先由样本中点过回归直线的结论求得1~6月份月用水费约为
的关系。(Ⅲ)先由样本中点过回归直线的结论求得1~6月份月用水费约为![]() 7月份的水费为
7月份的水费为![]() 元,再根据回归方程求得7月份的用水吨数。
元,再根据回归方程求得7月份的用水吨数。
试题解析:
(Ⅰ)由频率分布直方图可得该市居民每月的用水量的平均数为
![]()
![]() 。
。
设中位数为![]() ,
,
则![]() ,
,
解得![]() 。
。
(Ⅱ)设居民月用水量为![]() 吨,相应的水费为
吨,相应的水费为![]() 元,则由题意得
元,则由题意得
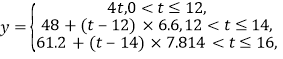
即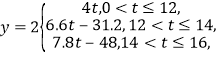
(Ⅲ)设李某2017年1~6月份月用水费![]() (元)与月份
(元)与月份![]() 的对应点为
的对应点为![]() ,它们的平均值分别为
,它们的平均值分别为![]() ,
,![]() ,
,
则![]() ,
,
又点![]() 在直线
在直线![]() 上,
上,
所以![]() ,
,
因此![]() ,
,
所以7月份的水费为![]() 元.
元.
由(2)知,当![]() 时,
时,![]() ,
,
所以李某7月份的用水吨数约为13吨.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 为坐标原点,
为坐标原点, ![]() 、
、![]() 是双曲线
是双曲线![]() 上的两个动点,动点
上的两个动点,动点![]() 满足
满足![]() ,直线
,直线![]() 与直线
与直线![]() 斜率之积为2,已知平面内存在两定点
斜率之积为2,已知平面内存在两定点![]() 、
、![]() ,使得
,使得![]() 为定值,则该定值为________
为定值,则该定值为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=a2x2(a>0),g(x)=bln x.
(1)若函数y=f(x)图象上的点到直线x-y-3=0距离的最小值为2![]() ,求a的值;
,求a的值;
(2)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=![]() ,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数M,使得函数
,存在一个正数M,使得函数![]() 的值域包含于区间[-M,M]。例如,当
的值域包含于区间[-M,M]。例如,当![]() ,
, ![]() 时,
时, ![]() ,现有如下命题:
,现有如下命题:
①设函数![]() 的定义域为D,则“
的定义域为D,则“![]() ”的充要条件是“
”的充要条件是“![]() ”;
”;
②若函数![]() ,则
,则![]() 有最大值和最小值;
有最大值和最小值;
③若函数![]() ,
, ![]() 的定义域相同,且
的定义域相同,且![]() ,
, ![]() ,则
,则![]()
④若函数![]() ,则
,则![]() 有最大值且
有最大值且![]() ,
,
其中的真命题有_____________。(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com