
分析 (1)由$\overrightarrow{m}$⊥$\overrightarrow{n}$,得(a+c)(a-c)+b(b-a)=0化简整理得a2+b2-c2=ab代入余弦定理即可求得cosC,结合C的范围进而求得C.
(2)由第二问得到的A与B的关系式,用A表示出B,代入所求的式子中,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据A的范围,求出此时正弦函数的值域,可得出所求式子的范围.
解答 解:$(1)由已知可得:_{\;}^{\;}({a+c})({a-c})+b({b-a})=0⇒{a^2}+{b^2}-{c^2}=ab$,
∴$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}=\frac{1}{2}$,
∵0<C<π,
∴$C=\frac{π}{3}$.
$(2)_{\;}^{\;}∵C=\frac{π}{3}$,
∴$A+B=\frac{2π}{3}$,
∴$sinA+sinB=sinA+sin({\frac{2π}{3}-A})=sinA+sin\frac{2π}{3}cosA-cos\frac{2π}{3}sinA$=$\frac{3}{2}sinA+\frac{{\sqrt{3}}}{2}cosA=\sqrt{3}({\frac{{\sqrt{3}}}{2}sinA+\frac{1}{2}cosA})=\sqrt{3}sin({A+\frac{π}{6}})$,
∵$0<A<\frac{2π}{3}$,
∴$\frac{π}{6}<A+\frac{π}{6}<\frac{5π}{6}⇒\frac{1}{2}<sin({A+\frac{π}{6}})≤1$,
∴$\frac{\sqrt{3}}{2}$<sinA+sinB=$\sqrt{3}$sin(A+$\frac{π}{6}$)≤$\sqrt{3}$.
则sinA+sinB的取值范围是($\frac{\sqrt{3}}{2}$,$\sqrt{3}$].
点评 此题考查了余弦定理,两角和与差的正弦函数公式,正弦函数的定义域与值域,以及特殊角的三角函数值,熟练掌握公式及定理是解本题的关键,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
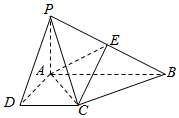 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三角形的内角是第一象限角或第二象限角 | |
| B. | 第一象限的角是锐角 | |
| C. | 第二象限的角比第一象限的角大 | |
| D. | 角α是第四象限角的充要条件是2kπ-$\frac{π}{2}$<α<2kπ(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{e}$ | B. | $\frac{1}{2}$ | C. | $\root{4e}{e}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0,则A=$\frac{π}{6}$.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是最大、最小值点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0,则A=$\frac{π}{6}$.查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
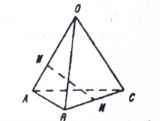
如图,空间四边形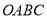 中,
中,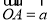 ,
,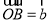 ,
,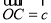 ,点
,点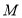 在
在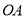 上,且
上,且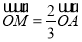 ,点
,点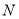 为
为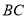 中点,则
中点,则 等于( )
等于( )
A.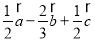 B.
B.
C.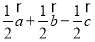 D.
D.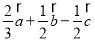
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,2\root{3}{3})$ | B. | $(2\root{3}{3},+∞)$ | C. | $(-2\root{3}{3},2\root{3}{3})$ | D. | $(0,2\root{3}{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com