
【题目】已知函数y=f(x)是R上的偶函数,对x∈R都有f(x+4)=f(x)+f(2)成立.当x1,x2∈[0,2],且x1≠x2时,都有![]() <0,给出下列命题:
<0,给出下列命题:
①f(2)=0;
②直线x=-4是函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[-4,4]上有四个零点;
④f(2 014)=0.
其中所有正确命题的序号为________.
【答案】①②④
【解析】令x=-2,得f(-2+4)=f(-2)+f(2),解得f(-2)=0,因为函数f(x)为偶函数,所以f(2)=0,①正确;因为f(-4+x)=f(-4+x+4)=f(x),f(-4-x)=f(-4-x+4)=f(-x)=f(x),所以f(-4+x)=f(-4-x),即x=-4是函数f(x)的一条对称轴,②正确;当x1,x2∈[0,2],且x1≠x2时,都有![]() <0,说明函数f(x)在[0,2]上是单调递减函数,又f(2)=0,因此函数f(x)在[0,2]上只有一个零点,由偶函数知函数f(x)在[-2,0]上也只有一个零点,由f(x+4)=f(x),知函数的周期为4,所以函数f(x)在(2,4]与[-4,-2)上也单调,因此,函数在[-4,4]上只有2个零点,③错;对于④,因为函数的周期为4,即有f(2)=f(6)=f(10)=…=f(2 014)=0,④正确.
<0,说明函数f(x)在[0,2]上是单调递减函数,又f(2)=0,因此函数f(x)在[0,2]上只有一个零点,由偶函数知函数f(x)在[-2,0]上也只有一个零点,由f(x+4)=f(x),知函数的周期为4,所以函数f(x)在(2,4]与[-4,-2)上也单调,因此,函数在[-4,4]上只有2个零点,③错;对于④,因为函数的周期为4,即有f(2)=f(6)=f(10)=…=f(2 014)=0,④正确.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项![]() ,
, ![]() 的部分项
的部分项![]() 、
、![]() 、 、
、 、![]() 恰为等比数列,且
恰为等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() (用
(用![]() 表示);
表示);
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() , 求证:
, 求证: ![]() (
(![]() 是正整数
是正整数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-![]() (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
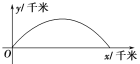
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分15分)在直三棱柱![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() 是棱
是棱![]() 的中点,且
的中点,且![]() .
.
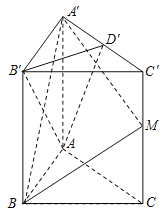
(1)试在棱![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ;
;
(2)当点![]() 在棱
在棱![]() 中点时,求直线
中点时,求直线![]() 与平面
与平面![]() 所成角的大小的正弦值。
所成角的大小的正弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com