
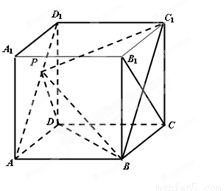
(本题满分14分)如图,在棱长为的正方体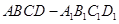 中,
中,
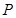 为线段
为线段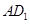 上的点,且满足
上的点,且满足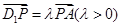 .
.
(Ⅰ)当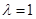 时,求证:平面
时,求证:平面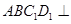 平面
平面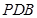 ;
;
(Ⅱ)试证无论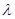 为何值,三棱锥
为何值,三棱锥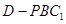 的体积恒为定值;
的体积恒为定值;
 (Ⅲ)求异面直线
(Ⅲ)求异面直线 与
与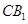 所成的角的余弦值.
所成的角的余弦值.
方法一、证明:(Ⅰ)∵正方体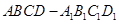 中,
中,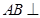 面
面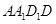 ,
,
又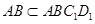 ∴平面
∴平面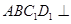 平面
平面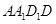 , ∵
, ∵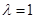 时,
时,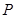 为
为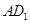 的中点,∴
的中点,∴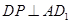 ,
又∵平面
,
又∵平面 平面
平面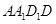
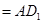 ,∴
,∴ 平面
平面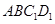 ,
,
又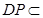 平面
平面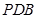 ,∴平面
,∴平面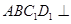 平面
平面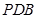 .……………5分
.……………5分
(Ⅱ)∵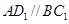 ,
,
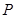 为线段
为线段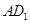 上的点,
上的点,
∴三角形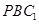 的面积为定值,即
的面积为定值,即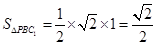 ,
,
又∵ 平面
平面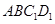 ∴点
∴点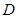 到平面
到平面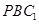 的距离为定值,
的距离为定值,
即 , ∴三棱锥
, ∴三棱锥 的体积为定值,
的体积为定值,
即 .
.
也即无论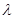 为何值,三棱锥
为何值,三棱锥 的体积恒为定值
的体积恒为定值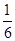 ; ……………10分
; ……………10分
(Ⅲ)∵由(Ⅰ)易知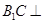 平面
平面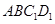 ,又
,又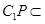 平面
平面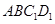 ,∴
,∴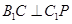 ,
即异面直线
,
即异面直线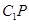 与
与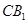 所成的角为定值
所成的角为定值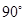 ,从而其余弦值为
,从而其余弦值为 .
……………14分
.
……………14分
方法二、如图,以点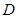 为坐标原点,建立如图所示的坐标系.
为坐标原点,建立如图所示的坐标系.
(Ⅰ)当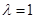 时,即点
时,即点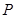 为线段
为线段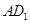 的中点,则
的中点,则 ,又
,又 、
、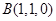

∴ ,
,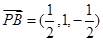 ,设平面
,设平面 的法向量为
的法向量为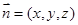 ……1分
……1分
则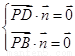 ,即
,即 ,令
,令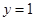 ,
,
解得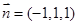 ,……2分
,……2分
又∵点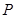 为线段
为线段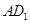 的中点,∴
的中点,∴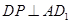 ,
,
∴ 平面
平面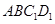 ,
,
∴平面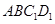 的法向量为
的法向量为 ,
………3分
,
………3分
∵ ,
,
∴平面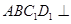 平面
平面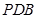 ,
………………………6分
,
………………………6分
(Ⅱ)略; ………………………10分
(Ⅲ)∵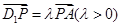 ,∴
,∴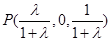 , ………………………11分
, ………………………11分
又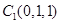 、
、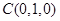 、
、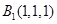 ,∴
,∴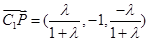 ,
, …12分
…12分
∵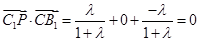 ……………………13分
……………………13分
∴不管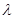 取值多少,都有
取值多少,都有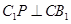 ,
,
即异面直线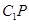 与
与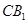 所成的角的余弦值为0.
……………14分
所成的角的余弦值为0.
……………14分
【解析】略


科目:高中数学 来源: 题型:
(本题满分14分)如图2,为了绿化城市,拟在矩形区域ABCD内建一个矩形草坪,另外△AEF内部有一文物保护区域不能占用,经过测量AB=100m,BC=80m,AE=30m,AF=20m,应该如何设计才能使草坪面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
如图,已知直三棱柱ABC—A1B1C1,![]() ,E是棱CC1上动点,F是AB中点,
,E是棱CC1上动点,F是AB中点,![]()
(1)求证:![]() ;
;
(2)当E是棱CC1中点时,求证:CF//平面AEB1;
(3)在棱CC1上是否存在点E,使得二面角A—EB1—B的大小是45°,若存在,求CE的长,若不存在,请说明理由。

查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省济宁市高三第二次月考文科数学 题型:解答题
(本题满分14分)如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4.

(Ⅰ)若F为DE的中点,求证:BE//平面ACF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值
查看答案和解析>>
科目:高中数学 来源:2011年福建省高二上学期期末考试数学理卷 题型:解答题
(本题满分14分)如图,正方形 、
、 的边长都是1,平面
的边长都是1,平面
 平面
平面 ,点
,点 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)

(I)求 的长;
的长;
(II) 为何值时,
为何值时, 的长最小;
的长最小;
(III)当 的长最小时,求面
的长最小时,求面 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.
查看答案和解析>>
科目:高中数学 来源:杭州市2010年第二次高考科目教学质量检测 题型:解答题
(本题满分14分)如图,矩形BCC1B1所在平面垂直于三角形ABC所在平面,BB1=CC1=AC=2, ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。
 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC;
(2)求证:平面 平面C1CBB1;
平面C1CBB1;
(3)求异面直线AB与EB1所成的角。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com