
分析 第一次摸出红球为事件A,第二次摸出红球为事件B,先分别求出P(A)和P(AB),由此能求出P(B|A).
解答 解:设第一次摸出红球为事件A,第二次摸出红球为事件B,
则P(A)=$\frac{6}{10}=\frac{3}{5}$,P(AB)=$\frac{{C}_{6}^{2}}{{C}_{10}^{2}}$=$\frac{1}{3}$.
∴P(B|A)=$\frac{P(AB)}{P(A)}$=$\frac{\frac{1}{3}}{\frac{3}{5}}$=$\frac{5}{9}$.
故答案为:$\frac{5}{9}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意条件概率公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
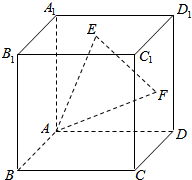 如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量:
如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com