分析:(I)欲证A1C∥平面AB1D,根据直线与平面平行的判定定理可知只需证MN与平面A1ABB1内一直线平行,连接A1B,设A1B∩AB1=E,连接DE,根据中位线定理可知DE∥A1C,DE?平面AB1D,A1C?平面AB1D,满足定理所需条件;
(II)作DF⊥AB于点F,作FG⊥AB1于点G,连接DG,根据二面角平面角的定义可知∠FGD是二面角B-AB1-D的平面角,
在Rt△DFG中,求出二面角B-AB1-D的大小即可.
解答: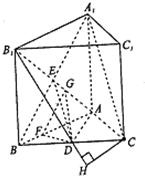
(I)证明:
连接A
1B,设A
1B∩AB
1=E,连接DE.
∵ABC-A
1B
1C
1是正三棱柱,且AA
1=AB,
∴四边形A
1ABB
1是正方形,
∴E是A
1B的中点,
又D是BC的中点,
∴DE∥A
1C.
∵DE?平面AB
1D,A
1C?平面AB
1D,
∴A
1C∥平面AB
1D.
(II)解:在面ABC内作DF⊥AB于点F,在面A
1ABB
1内作FG⊥AB
1于点G,连接DG.
∵平面A
1ABB
1⊥平面ABC,∴DF⊥平面A
1ABB
1,
∴FG是DG在平面A
1ABB
1上的射影,∵FG⊥AB
1,∴DG⊥AB
1∴∠FGD是二面角B-AB
1-D的平面角
设A
1A=AB=1,在正△ABC中,DF=
.
在△ABE中,
FG=•BE=,
在Rt△DFG中,
tanFGD==,
所以,二面角B-AB
1-D的大小为
arctan.
点评:本小题主要考查直线与平面的位置关系、二面角及其平面角等有关知识,考查空间想象能力和思维能力,属于中档题.

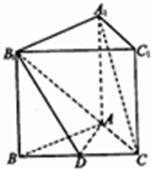 如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (I)证明:
(I)证明:

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案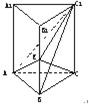 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.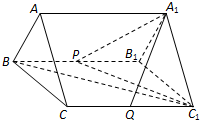 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.