
【题目】已知定义在R的函数![]() 是偶函数,且满足
是偶函数,且满足![]() 上的解析式为
上的解析式为![]() ,过点
,过点![]() 作斜率为k的直线l,若直线l与函数
作斜率为k的直线l,若直线l与函数![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 为坐标原点,
为坐标原点, ![]() 、
、![]() 是双曲线
是双曲线![]() 上的两个动点,动点
上的两个动点,动点![]() 满足
满足![]() ,直线
,直线![]() 与直线
与直线![]() 斜率之积为2,已知平面内存在两定点
斜率之积为2,已知平面内存在两定点![]() 、
、![]() ,使得
,使得![]() 为定值,则该定值为________
为定值,则该定值为________
查看答案和解析>>
科目:高中数学 来源: 题型:
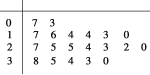
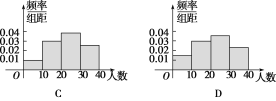
【题目】某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=a2x2(a>0),g(x)=bln x.
(1)若函数y=f(x)图象上的点到直线x-y-3=0距离的最小值为2![]() ,求a的值;
,求a的值;
(2)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=![]() ,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com